Càlcul de l'element calefactor

Per determinar un dels paràmetres principals del cable de l'element de calefacció - diàmetre d, m (mm), s'utilitzen dos mètodes de càlcul: d'acord amb la potència de superfície específica admissible PF i utilitzant la taula de càrregues actuals.

Potència superficial específica permesa PF= P⁄F,

on P és la potència de l'escalfador de filferro, W;

F = π ∙ d ∙ l — àrea de l'escalfador, m2; l - longitud del cable, m.

Segons el primer mètode

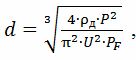
on ρd — resistència elèctrica del material del cable a la temperatura real, Ohm • m; U és la tensió del cable de l'escalfador, V; PF: valors permesos de potència superficial específica per a diferents escalfadors:

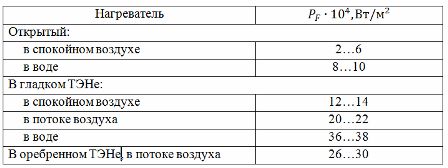
El segon mètode utilitza una taula de càrregues actuals (vegeu la taula 1) compilada a partir de dades experimentals. Per utilitzar la taula indicada, cal determinar la temperatura de calefacció calculada Tp relacionada amb la temperatura real (o admissible) del conductor Td mitjançant la relació:

Tr = Km ∙ Ks ∙ Td,

on Km és el factor d'instal·lació, tenint en compte el deteriorament de les condicions de refrigeració de l'escalfador a causa de la seva construcció; Kc és el factor ambiental, tenint en compte la millora de les condicions de refrigeració de l'escalfador en comparació amb un ambient d'aire estacionari.

Per a un element de calefacció fet de filferro retorçat en espiral, Km = 0,8 … 0,9; el mateix, amb una base ceràmica Km = 0,6 ... 0,7; per a un cable de plaques calefactores i alguns elements calefactors Km = 0,5 ... 0,6; per a un conductor d'un terra elèctric, sòl i elements de calefacció Km = 0,3 ... 0,4. Un valor menor de Km correspon a un escalfador amb un diàmetre menor, un valor més gran a un diàmetre més gran.

Quan es treballa en condicions diferents de la convecció lliure, es pren Kc = 1,3 … 2,0 per als elements de calefacció en el corrent d'aire; per als elements en aigua tranquil·la Kc = 2,5; al cabal d'aigua — Kc = 3,0 … 3,5.

Si s'estableix la tensió Uph i la potència Pf del futur escalfador (dissenyat), llavors el seu corrent (per fase)

Iph = Pph⁄Uph

Segons el valor calculat del corrent de l'escalfador per a la temperatura calculada necessària del seu escalfament segons la taula 1, es troba el diàmetre requerit del cable de nicrom d i la longitud requerida del cable, m, per a la fabricació de l'escalfador. es calcula:

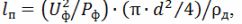
on d és el diàmetre del cable seleccionat, m; ρd és la resistència elèctrica específica del conductor a la temperatura d'escalfament real, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

on αр — coeficient de resistència a la temperatura, 1/OS.

Per determinar els paràmetres de l'espiral de nicrom, prenem el diàmetre mitjà de les espires D = (6 … 10) ∙ d, el pas de l'espiral h = (2 … 4) ∙ d,

nombre de voltes

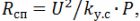
longitud de l'hèlix lsp = h ∙ n.

En calcular els elements de calefacció, cal recordar que la resistència del cable espiral després de prémer l'element de calefacció

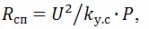
on k (y.s) és un coeficient que té en compte la reducció de la resistència de l'espiral; segons dades experimentals, k (s) = 1,25. També s'ha de tenir en compte que la potència superficial específica del cable espiral és 3,5 ... 5 vegades més gran que la potència superficial específica de l'element de calefacció tubular.

En els càlculs pràctics de l'element calefactor, primer determineu la temperatura de la seva superfície Tp = To + P ∙ Rt1,

on és la temperatura ambient, °C; P és la potència de l'element calefactor, W; RT1 - resistència tèrmica a la canonada - interfície mitjana, ОC / W.

Aleshores es determina la temperatura del bobinatge: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

on Rt2 és la resistència tèrmica de la paret de la canonada, ОC / W; RT3 - resistència tèrmica del farciment, ОC / W; Rp1 = 1⁄ (α ∙ F), on α és el coeficient de transferència de calor, W / (m ^ 2 • ОС); F - àrea de l'escalfador, m2; Rt2 = δ⁄ (λ ∙ F), on δ és el gruix de la paret, m; λ — conductivitat tèrmica de la paret, W / (m • ОС).

Per obtenir més informació sobre el dispositiu dels elements de calefacció, consulteu aquí: Elements de calefacció. Dispositiu, selecció, funcionament, connexió d'elements de calefacció

Taula 1. Taula de càrregues actuals

Exemple 1. Calculeu l'escalfador elèctric en forma d'espiral de filferro segons la potència superficial específica admissible PF.

Condició.Potència de l'escalfador P = 3,5 kW; tensió d'alimentació U = 220 V; material del filferro — nicrom Х20Н80 (un aliatge de 20% de crom i 80% de níquel), per tant, la resistència elèctrica específica del cable ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; coeficient de temperatura de resistència αр = 16 ∙ 10 ^ (- 6) 1 /ОС; l'espiral és oberta, en forma metàl·lica, la temperatura de treball de l'espiral és Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Determineu d, lp, D, h, n, lp.

Respon. Resistència de la bobina: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohms.

Resistència elèctrica específica a Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Trobeu el diàmetre del cable:

De l'expressió R = (ρ ∙ l) ⁄S obtenim l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), d'on la longitud del cable

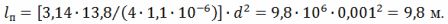
El diàmetre mitjà del gir en espiral és D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Pas de l'espiral h = 3 ∙ d = 3 ∙ 1 = 3 mm.

El nombre de voltes de l'espiral

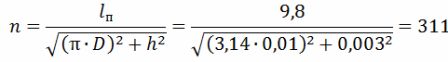
La longitud de l'hèlix és lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Exemple 2. Calculeu estructuralment l'escalfador de resistència del cable en determinar el diàmetre del cable d utilitzant la taula de càrregues actuals (vegeu la taula 1).

Condició. Potència de l'escalfador de filferro P = 3146 W; tensió d'alimentació U = 220 V; material del filferro — nicrom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; hèlix oberta situada al corrent d'aire (Km = 0,85, Kc = 2,0); temperatura de funcionament admissible del conductor Td = 470 ОС.

Determineu el diàmetre d i la longitud del fil lp.

Respon.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

El corrent de l'escalfador de disseny I = P⁄U = 3146⁄220 = 14,3 A.

Segons la taula de càrregues actuals (vegeu la taula 1) a Tр = 800 ОС i I = 14,3 A, trobem el diàmetre i la secció transversal del cable d = 1,0 mm i S = 0,785 mm2.

Longitud del cable lp = (R ∙ S) ⁄ρ800,

on R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = ∙ 1.1 ] 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

També, si cal, semblant al primer exemple, es poden definir D, h, n, lsp.

Exemple 3. Determineu la tensió admissible de l'escalfador elèctric tubular (TEN).

Estat... La bobina de l'element calefactor està feta de filferro de nicrom amb un diàmetre d = 0,28 mm i una longitud l = 4,7 m L'element calefactor està en aire tranquil amb una temperatura de 20 °C. Característiques del nicrom: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. La longitud de la part activa de la carcassa de l'element de calefacció és La = 40 cm.

L'element de calefacció és llis, diàmetre exterior dob = 16 mm. Coeficient de transferència de calor α = 40 W / (m ^ 2 ∙ ° C). Resistències tèrmiques: farciment RT3 = 0,3 ОС / W, parets de l'habitatge Rт2 = 0,002 ОС / W.

Determineu quina tensió màxima es pot aplicar a l'element de calefacció perquè la seva temperatura de la bobina Tsp no superi els 1000 ℃.

Respon. Temperatura de l'element de calefacció de l'element de calefacció

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

on és la temperatura de l'aire ambient; P és la potència de l'element calefactor, W; RT1: resistència tèrmica de contacte de la interfície tub-medi.

Potència de l'element calefactor P = U ^ 2⁄R,

on R és la resistència de la bobina de calefacció.Per tant, podem escriure Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), d'on la tensió a l'element de calefacció

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Trobeu R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

on ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ^∙ 1,12 ∙ — 6) Ohm • m.

Aleshores R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Resistència tèrmica de contacte RT1 = 1⁄ (α ∙ F),

on F és l'àrea de la part activa de la carcassa de l'element de calefacció; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Trobeu Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Determineu la tensió de l'element calefactor U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Si la tensió nominal indicada a l'element calefactor és de 220 V, la sobretensió a Tsp = 1000 OS serà del 5,6% ∙ Un.