Caiguda de tensió

Conceptes i fórmules

A cada resistència r, quan passa el corrent I, apareix una tensió U = I ∙ r, que se sol anomenar caiguda de tensió d'aquesta resistència.

Si només hi ha una resistència r al circuit, tota la tensió de la font Ust cau sobre aquesta resistència.

Si el circuit té dues resistències r1 i r2 connectades en sèrie, aleshores la suma de les tensions de les resistències U1 = I ∙ r1 i U2 = I ∙ r2, és a dir. la caiguda de tensió és igual a la tensió de la font: Ust = U1 + U2.

La tensió d'alimentació és igual a la suma de les caigudes de tensió del circuit (segona llei de Kirchhoff).

Exemples de

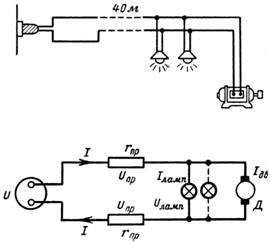
1. Quina caiguda de tensió es produeix a través del filament de la làmpada amb resistència r = 15 Ohm quan passa el corrent I = 0,3 A (Fig. 1)?

Arròs. 1.

El nombre de caigudes de tensió Llei d'Ohm: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

La tensió entre els punts 1 i 2 de la làmpada (vegeu l'esquema) és de 4,5 V. La làmpada s'encén normalment si hi passa el corrent nominal o si hi ha una tensió nominal entre els punts 1 i 2 (s'indiquen el corrent nominal i la tensió). al llum).

2. Es connecten en sèrie dues bombetes idèntiques per a una tensió de 2,5 V i un corrent de 0,3 A i es connecten a una bateria de butxaca amb una tensió de 4,5 V. Quina caiguda de tensió es genera als terminals de les bombetes individuals (Fig. 2). ))?

Arròs. 2.

Les bombetes idèntiques tenen la mateixa resistència r. Quan estan connectats en sèrie, hi circula el mateix corrent I. D'això se'n dedueix que tindran les mateixes caigudes de tensió, la suma d'aquestes tensions ha de ser igual a la tensió de la font U = 4,5 V. Cada bombeta té una tensió de 4 , 5: 2 = 2,25 V.

Podeu resoldre aquest problema i el càlcul seqüencial. Calculem la resistència de la bombeta segons les dades: rl = 2,5 / 0,3 = 8,33 Ohm.

Corrent del circuit I = U / (2rl) = 4,5 / 16,66 = 0,27 A.

La caiguda de tensió a la bombeta U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. La tensió entre el carril i el cable de contacte de la línia del tramvia és de 500 V. Per a la il·luminació s'utilitzen quatre làmpades idèntiques connectades en sèrie. Per a quina tensió s'ha de seleccionar cada llum (Fig. 3)?

Arròs. 3.

Les làmpades idèntiques tenen resistències iguals per les quals passa el mateix corrent. La caiguda de tensió a les làmpades també serà la mateixa. Això vol dir que per a cada làmpada hi haurà 500: 4 = 125 V.

4. Es connecten en sèrie dues làmpades amb una potència de 40 i 60 W amb una tensió nominal de 220 V i es connecten a una xarxa amb una tensió de 220 V. Quina caiguda de tensió es produeix a cadascun d'ells (fig. 4)?

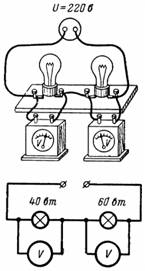
Arròs. 4.

La primera làmpada té una resistència r1 = 1210 Ohm, i la segona r2 = 806,6 Ohm (en estat d'escalfament). El corrent que passa per les làmpades és I = U / (r1 + r2) = 220 / 2016,6 = 0,109 A.

Caiguda de tensió a la primera làmpada U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Caiguda de tensió a la segona làmpada U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

Una làmpada amb una resistència més alta té una caiguda de tensió més gran i viceversa. Els filaments d'ambdues làmpades són molt febles, però la làmpada de 40 W és lleugerament més forta que la de 60 W.

5. Perquè la tensió del motor elèctric D (Fig. 5) sigui igual a 220 V, la tensió a l'inici de la línia llarga (a la central elèctrica) ha de ser superior a 220 V. caiguda de tensió (pèrdua) en línia. Com més gran sigui la resistència de la línia i el corrent, més gran serà la caiguda de tensió al llarg de la línia.

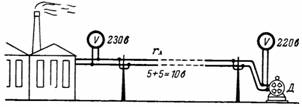Arròs. 5.

En el nostre exemple, la caiguda de tensió a cada cable de la línia és de 5 V. Aleshores, la tensió a les barres de la central elèctrica hauria de ser igual a 230 V.

6. El consumidor s'alimenta amb una bateria de 80 V amb un corrent de 30 A. Per al funcionament normal del consumidor, es permet una caiguda de tensió del 3% en cables d'alumini amb una secció transversal de 16 mm2. Quina és la distància màxima de la bateria a l'usuari?

Caiguda de tensió admissible a la línia U = 3/100 ∙ 80 = 2,4 V.

La resistència dels cables està limitada per la caiguda de tensió admissible rpr = U / I = 2,4 / 30 = 0,08 Ohm.

Utilitzant la fórmula per determinar la resistència, calculem la longitud dels cables: r = ρ ∙ l / S, a partir d'on l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Si l'usuari es troba a 22 m de la bateria, la tensió serà inferior a 80 V al 3%, és a dir. igual a 77,6 V.

7. Una línia telegràfica de 20 km de llarg està feta de filferro d'acer amb un diàmetre de 3,5 mm. La línia de retorn es substitueix per una presa de terra mitjançant barres metàl·liques. La resistència de la transició entre el bus i el terra és rz = 50 Ohm.Quina ha de ser la tensió de la bateria al principi de la línia si la resistència del relé al final de la línia és рп = 300 Ohm i el corrent del relé és I = 5 mA?

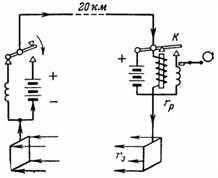
Arròs. 6.

El diagrama de connexió es mostra a la fig. 6. Quan es prem l'interruptor del telègraf en el punt d'enviament del senyal, el relé al punt receptor al final de la línia atrau l'induït K, que al seu torn encén la bobina de la gravadora amb el seu contacte. La tensió de sortida ha de compensar la caiguda de tensió a la línia, el relé receptor i les resistències transitòries de les barres de terra: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = I ∙ (rр + рр + 2 ∙ rр).

La tensió de la font és igual al producte del corrent per la resistència total del circuit.

Secció del cable S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Resistència de línia rl = ρ ∙ l / S = 0,11 ∙ 20.000 / 9,6 = 229,2 ohms.

Resistència resultant r = 229,2 + 300 + 2 ∙ 50 = 629,2 Ohm.

Tensió de sortida U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.

La caiguda de tensió a la línia durant el pas d'un corrent I = 0,005 A serà: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

La caiguda de tensió relativament baixa a la línia s'aconsegueix a causa del baix valor del corrent (5 mA). Per tant, al punt receptor hi ha d'haver un relé sensible (amplificador), que s'encén per un pols feble de 5 mA i mitjançant el seu contacte s'encén un altre relé més potent.

8. Quina és la tensió de les làmpades del circuit de la fig. 28, quan: a) el motor no està engegat; b) el motor arrenca; c) el motor està en marxa.

El motor i 20 llums estan connectats a una xarxa de 110 V. Els llums estan dissenyats per a 110 V i 40 W. El corrent d'arrencada del motor és Ip = 50 A i la seva intensitat nominal és In = 30 A.

El fil de coure introduït té una secció transversal de 16 mm2 i una longitud de 40 m.

Fig. 7 i les condicions del problema, es pot veure que el corrent del motor i la làmpada fa que la tensió de la línia caigui, per tant, la tensió de càrrega serà inferior a 110 V.

Arròs. 7.

U = 2 ∙ Ul + Ulamp.

Per tant, la tensió a les làmpades Ulamp = U-2 ∙ Ul.

Cal determinar la caiguda de tensió a la línia a diferents corrents: Ul = I ∙ rl.

Resistència de tota la línia

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

El corrent que passa per totes les làmpades

20 ∙ Ilamp = 20 ∙ 40/110 = 7,27 A.

Caiguda de tensió de la xarxa quan només els llums estan encesos (sense motor),

2 ∙ Ul = Ilamp ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

La tensió a les làmpades en aquest cas és:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

Quan s'engega el motor, els llums brillaran més tènument, ja que la caiguda de tensió a la línia és més gran:

2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

La tensió mínima dels llums a l'arrencada del motor serà:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9V.

Quan el motor està en marxa, la caiguda de tensió a la línia és menor que quan s'engega el motor, però més que quan el motor està apagat:

2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

La tensió de les làmpades durant el funcionament normal del motor és:

Ulamp = 110-3,32 = 106,68 V.

Fins i tot una lleugera disminució de la tensió de les làmpades en relació amb el nominal afecta significativament la brillantor de la il·luminació.