Força de tracció dels electroimants

La força amb què un electroimant atrau materials ferromagnètics depèn del flux magnètic F o, equivalentment, de la inducció B i de l'àrea de la secció transversal de l'electroimant S.

La força de pressió de l'electroimant ve determinada per la fórmula

F = 40550 ∙ B ^ 2 ∙ S,

on F és la força de pressió de l'electroimant, kg (la força també es mesura en newtons, 1 kg = 9,81 N o 1 N = 0,102 kg); B — inducció, T; S és l'àrea de la secció transversal de l'electroimant, m2.

Exemples de

1. L'electroimant de l'aixeta és un circuit magnètic (Fig. 1). Quina és la força d'elevació d'un electroimant de grua de ferradura, si la inducció magnètica és B = 1 T i l'àrea de la secció transversal de cada pol de l'electroimant és S = 0,02 m2 (Fig. 1, b)? Descuidar l'efecte de la bretxa entre l'electroimant i l'induït.

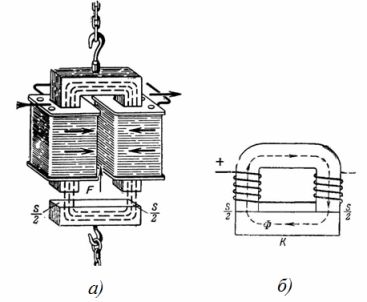
Arròs. 1. Electroimant elevador

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

2. Un electroimant circular d'acer té les dimensions que es mostren a la fig. 2, a i b. La força d'elevació de l'electroimant és de 3 T. Determineu l'àrea de la secció transversal del nucli de l'electroimant, n. p. i el nombre de voltes de la bobina amb un corrent de magnetització I = 0,5 A.

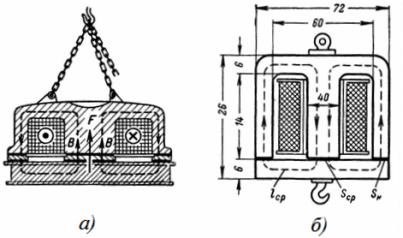
Arròs. 2. Electroimant rodó

El flux magnètic passa pel nucli interior circular i torna pel cos cilíndric. Les àrees de secció transversal del nucli Sc i la carcassa Sk són aproximadament les mateixes, per tant, els valors d'inducció en el nucli i la carcassa són pràcticament els mateixos:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

La inducció requerida a l'electroimant ve determinada per la fórmula F = 40550 ∙ B ^ 2 ∙ S,

on B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

La tensió en aquesta inducció es troba a la corba de magnetització de l'acer fos:

H = 180 A/m.

La longitud mitjana de la línia de camp (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Força magnetitzant I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

En realitat n. s, és a dir, el corrent i el nombre de voltes, han de ser moltes vegades més grans, ja que hi ha un espai d'aire inevitable entre l'electroimant i l'induït, que augmenta significativament la resistència magnètica del circuit magnètic. Per tant, s'ha de tenir en compte l'entrefer a l'hora de calcular els electroimants.

3. La bobina de l'electroimant de l'aixeta té 1350 voltes, hi circula un corrent I = 12 A. Les dimensions de l'electroimant es mostren a la fig. 3. Quin pes aixeca l'electroimant a una distància d'1 cm de l'induït i quin pes pot aguantar després de la gravetat?

Arròs. 3. Bobina electromagnètica

La major part de N. amb I ∙ ω es gasta en conduir el flux magnètic a través de l'entrefer: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Força de magnetització I ∙ ω = 12 ∙ 1350 = 16200 A.

Com que H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, aleshores Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Per tant, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, és a dir. B = 1,012T.

Suposem que la inducció és B = 1 T, ja que part de n. c. I ∙ ω es gasta en la conducció del flux magnètic a l'acer.

Comprovem aquest càlcul mitjançant la fórmula I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

La longitud mitjana de la línia magnètica és: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

La intensitat Hc a B = 1 T (10000 Gs) es determina a partir de la corba de magnetització:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

La força de magnetització I ∙ ω = 16114 Av creant una inducció B = 1 T és pràcticament igual a n donat. v. I ∙ ω = 16200 Av.

L'àrea de la secció transversal total del nucli i del con és: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

L'electroimant atraurà una càrrega de pes F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg des d'una distància d'1 cm.

Com que l'espai d'aire pràcticament desapareix després d'atreure l'armadura, l'electroimant pot suportar una càrrega molt més gran. En aquest cas, tot el n. c. I ∙ ω es gasta en la conducció del flux magnètic només en acer, per tant I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Amb aquesta tensió, l'acer està pràcticament saturat i la inducció en ell és d'aproximadament 2 T. L'electroimant atrau l'induït amb una força F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. El relé de senyal (intermitent) consta d'un electroimant blindat 1 amb un nucli rodó i una armadura de tipus vàlvula 2, que, després de subministrar corrent a l'electroimant, atrau i allibera l'intermitent 3, que obre el dígit del senyal (Fig. 4).

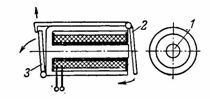
Arròs. 4. Armadura electroimant

La força de magnetització és I ∙ ω = 120 Av, l'entrefer és δ = 0,1 cm i l'àrea de la secció transversal total de l'electroimant és S = 2 cm2. Estimar la força de tracció del relé.

La inductància B es determina mitjançant aproximacions successives utilitzant l'equació I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Sigui n. c. Hc ∙ lc és 15% I ∙ ω, és a dir. 18 Av.

Aleshores I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Per tant trobem la inducció B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51.000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Després de substituir el valor B a la fórmula F = 40550 ∙ B ^ 2 ∙ S, obtenim:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

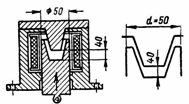
5. El solenoide de fre de corrent continu (Fig. 5) té una armadura de pistó amb un toc cònic. La distància entre l'induït i el nucli és de 4 cm El diàmetre de treball (nuclis amb àrea de contacte circular) d = 50 mm. L'induït s'entra a la bobina amb una força de 50 kg. La longitud de la línia mitjana de força lav = 40 cm Determineu n. pp i el corrent de la bobina si hi ha 3000 espires.

Arròs. 5. Solenoide de fre de corrent continu

L'àrea de la secció de treball de l'electroimant és igual a l'àrea d'un cercle amb un diàmetre d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

La inducció B necessària per crear una força F = 50 kg es troba a partir de l'equació F = 40550 ∙ B ^ 2 ∙ S,

on B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Força magnetitzant I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Determinem la força de magnetització de l'acer Hc ∙ lc de manera simplificada, basant-nos en el fet que és del 15% I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Av.

Corrent de magnetització I = (I ∙ ω) / ω = 30000/3000 = 10 A.