Rigidesa dielèctrica de l'aïllament. Exemples de càlcul

Amb un augment gradual de la tensió U entre conductors separats per un dielèctric (aïllament), per exemple, plaques de condensadors o cables conductors, la intensitat (intensitat) del camp elèctric en el dielèctric augmenta. La força del camp elèctric en el dielèctric també augmenta a mesura que disminueix la distància entre els cables.

A una certa intensitat de camp, es produeix una ruptura en el dielèctric, es forma una espurna o arc i apareix un corrent elèctric al circuit. La força del camp elèctric en què es produeix la ruptura de l'aïllament s'anomena força elèctrica Epr de l'aïllament.

La rigidesa dielèctrica es defineix com la tensió per mm de gruix d'aïllament i es mesura en V/mm (kV/mm) o kV/cm. Per exemple, la rigidesa dielèctrica de l'aire entre plaques llises és de 32 kV / cm.

La força del camp elèctric en un dielèctric per al cas quan els conductors tenen forma de plaques o tires separades per un buit igual (per exemple, en un condensador de paper) es calcula mitjançant la fórmula

E = U/d,

on U és la tensió entre els cables, V (kV); d — gruix de la capa dielèctrica, mm (cm).

Exemples de

1. Quina és la intensitat del camp elèctric a l'entrefer de 3 cm de gruix entre les plaques si la tensió entre elles és U = 100 kV (Fig. 1)?

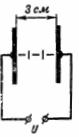
Arròs. 1.

La intensitat del camp elèctric és: E = U / d = 100000/3 = 33333 V / cm.

Aquesta tensió supera la rigidesa dielèctrica de l'aire (32 kV / cm) i hi ha risc de destrucció.

El risc de danys en corrent continu es pot prevenir augmentant l'espai fins, per exemple, 5 cm, o utilitzant un altre aïllament més fort en comptes de l'aire, com el cartró elèctric (Fig. 2).

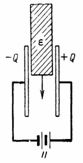
Arròs. 2.

El cartró elèctric té una constant dielèctrica de ε = 2 i una rigidesa dielèctrica de 80.000 V/cm. En el nostre cas, la intensitat del camp elèctric en l'aïllament és de 33333 V. L'aire no pot suportar aquesta força, mentre que el cartró elèctric en aquest cas té una reserva de rigidesa dielèctrica de 80.000/33333 = 2,4, ja que la rigidesa dielèctrica de la caixa elèctrica és 80.000/32.000 = 2,5 vegades la de l'aire.

2. Quina és la intensitat del camp elèctric en el dielèctric d'un condensador de 3 mm de gruix si el condensador està connectat a una tensió U = 6 kV?

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Un dielèctric amb un gruix de 2 mm es trenca a una tensió de 30 kV. Quina era la seva força elèctrica?

E = U / d = 30.000 / 0,2 = 150.000 V / cm = 150 kV / cm. El vidre té aquesta força elèctrica.

4. L'espai entre les plaques del condensador s'omple amb capes de cartró elèctric i una capa de mica del mateix gruix (Fig. 3). La tensió entre les plaques del condensador és U = 10000 V. El cartró elèctric té una constant dielèctrica ε1 = 2 i mica ε2 = 8.Com es distribuirà la tensió U entre les capes d'aïllament i quina intensitat tindrà el camp elèctric a les capes individuals?

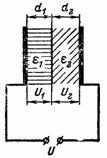
Arròs. 3.

Les tensions U1 i U2 a través de capes dielèctriques del mateix gruix no seran iguals. La tensió del condensador es dividirà en tensions U1 i U2, que seran inversament proporcionals a les constants dielèctriques:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Com que U = U1 + U2, tenim dues equacions amb dues incògnites.

Substitueix la primera equació a la segona: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Per tant, 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000V.

Tot i que les capes dielèctriques tenen el mateix gruix, no tenen la mateixa càrrega. Un dielèctric amb una constant dielèctrica més alta està menys carregat (U2 = 2000 V) i viceversa (U1 = 8000 V).

La intensitat del camp elèctric E a les capes dielèctriques és igual a:

E1 = U1 / d1 = 8000 / 0,2 = 40.000 V / cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

La diferència en la constant dielèctrica condueix a un augment de la intensitat del camp elèctric. Si tot el buit s'ompligués només amb un dielèctric, per exemple, mica o cartró elèctric, la intensitat del camp elèctric seria menor, ja que es distribuiria de manera bastant uniforme a l'espai:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

Per tant, cal evitar l'ús d'aïllaments complexos amb constants dielèctriques molt diferents. Per la mateixa raó, el risc de fallada augmenta quan es formen bombolles d'aire a l'aïllament.

5. Determineu la intensitat del camp elèctric en el dielèctric del condensador a partir de l'exemple anterior si el gruix de les capes dielèctriques no és el mateix.El quadre elèctric té un gruix d1 = 0,2 mm i mica d2 = 3,8 mm (Fig. 4).

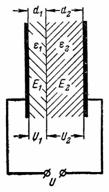
Arròs. 4.

La intensitat del camp elèctric es distribuirà inversament proporcional a les constants dielèctriques:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Com que E1 = U1 / d1 = U1 / 0,2 i E2 = U2 / d2 = U2 / 3,8, aleshores E1 / E2 = (U1 / 0,2) / (U2 / 3,8) = (U1 ∙ 3,8) / (0,2 ∙ U2) = 19 ∙ U1 / U2.

Per tant, E1 / E2 = 4 = 19 ∙ U1 / U2, o bé U1 / U2 = 4/19.

La suma de les tensions U1 i U2 de les capes dielèctriques és igual a la tensió de la font U: U = U1 + U2; 10000 = U1 + U2.

Com que U1 = 4/19 ∙ U2, aleshores 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190.000 /23 = 8260 V; U1 = U-U2 = 1740V.

La força del camp elèctric en mica és E2 ∙ 8260 / 3,8≈2174 V / cm.

La mica té una força elèctrica de 80.000 V/mm i pot suportar aquesta tensió.

La intensitat del camp elèctric en el cartró elèctric és E1 = 1740 / 0,2 = 8700 V / mm.

El cartró elèctric no suportarà aquesta tensió, ja que la seva rigidesa dielèctrica és només de 8000 V / mm.

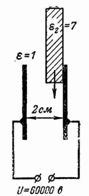
6. Es connecta una tensió de 60.000 V a dues plaques metàl·liques separades 2 cm.Determineu la intensitat del camp elèctric a l'entrefer, així com la intensitat del camp elèctric a l'aire i el vidre si hi ha vidre a l'espai insereix una placa amb un gruix d'1 cm (Fig. 5).

Arròs. 5.

Si només hi ha aire entre les plaques, la intensitat del camp elèctric és igual a: E = U / d = 60.000 /2 = 30.000 V / cm.

La intensitat del camp és propera a la rigidesa dielèctrica de l'aire.Si s'introdueix a l'espai una placa de vidre d'1 cm de gruix (constante dielèctrica de vidre ε2 = 7), aleshores E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60.000-U2; 8 ∙ U2 = 60.000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

La força del camp elèctric al vidre és E2 = 7,5 kV / cm, i la seva força elèctrica és de 150 kV / cm.

En aquest cas, el vidre té un factor de seguretat de 20 vegades.

Per a l'entrefer tenim: U1 = 60.000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

En aquest cas, la força del camp elèctric a l'entrefer és més gran que en el primer, sense vidre. Després d'introduir el vidre, tota la combinació té menys força que l'aire sol.

El risc de trencament també es produeix quan el gruix de la placa de vidre és igual a l'espai entre les plaques conductores, és a dir. 2 cm, ja que inevitablement hi haurà buits d'aire prims a l'espai que es punxarà.

La rigidesa dielèctrica de l'espai entre els conductors d'alta tensió s'ha de reforçar amb materials que tinguin una constant dielèctrica baixa i una rigidesa dielèctrica elevada, per exemple, cartró elèctric amb ε = 2. Evitar combinacions de materials amb una constant dielèctrica elevada (vidre). , porcellana) i aire, que cal substituir per oli.