Oscil·lacions contínues i ressonància paramètrica

Vibracions contínues: vibracions l'energia de les quals no canvia amb el temps. En els sistemes físics reals, sempre hi ha causes que provoquen la transició de l'energia vibratòria a l'energia tèrmica (per exemple, fricció en sistemes mecànics, resistència activa en sistemes elèctrics).

Per tant, només es poden obtenir oscil·lacions no amortides sempre que aquestes pèrdues d'energia es repoguin. Aquesta reposició es produeix automàticament en sistemes auto-oscil·lants a causa de l'energia d'una font externa. Les oscil·lacions electromagnètiques contínues són molt utilitzades. Per obtenir-los s'utilitzen diferents generadors.

Per fer que les vibracions elèctriques o mecàniques (d'un cercle oscil·lant o pèndol) no es puguin amortir, cal compensar en tot moment les pèrdues de resistència o per fricció.

Per exemple, podeu actuar sobre el circuit oscil·lant amb un EMF altern, que augmentarà periòdicament el corrent a la bobina i, en conseqüència, mantindrà l'amplitud de tensió al condensador.O podeu empènyer el pèndol d'una manera similar, mantenint-lo balancejant harmònicament.

Com sabeu, la magnitud de l'energia del camp magnètic de la bobina del circuit oscil·lant està relacionada amb la seva inductància i corrent mitjançant la següent relació (la segona fórmula ésenergia del camp elèctric del condensador mateix contorn)

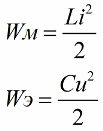
Des de la primera fórmula queda clar que si augmentem periòdicament el corrent a la bobina, actuant sobre el circuit EMF altern, aleshores (en augmentar o disminuir el segon factor de la fórmula - el corrent) periòdicament omplirem aquest circuit amb energia.

Actuant sobre el circuit estrictament en el temps amb les seves oscil·lacions lliures naturals, és a dir, a la freqüència de ressonància, obtindrem el fenomen de la ressonància elèctrica, perquè és a la freqüència de ressonància. sistema oscil·lant absorbeix de manera més intensa l'energia que se li subministra.

Però, què passa si canvieu periòdicament no el segon factor (no el corrent ni la tensió), sinó el primer factor: la inductància o la capacitat? En aquest cas, el circuit també patirà un canvi en la seva energia.

Per exemple, empenyent periòdicament el nucli dins i fora de la bobina o empènyer i sortir del condensadordielèctric, — també obtenim un canvi periòdic molt definit en l'energia del circuit.

Escrivim aquesta posició per a un canvi unitari en la inductància de la bobina:

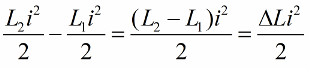
L'efecte més pronunciat del swing del circuit serà si els canvis d'inductància es fan just a temps. Per exemple, si agafem el mateix circuit en qualsevol moment del temps, quan ja hi circula una mica de corrent i i introduïm un nucli a la bobina, aleshores l'energia canviarà en la quantitat següent:

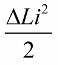
Ara deixeu que apareguin oscil·lacions lliures al propi circuit, però en el moment en què, després d'un quart de període, l'energia hagi passat completament al condensador i el corrent de la bobina s'hagi convertit en zero, retirarem bruscament el nucli de la bobina La inductància tornarà al seu estat original, al valor inicial L. No cal gastar cap treball contra el camp magnètic quan s'elimina el nucli. Per tant, quan el nucli es va empènyer a la bobina, el circuit va rebre energia, ja que vam treballar, el valor de la qual:

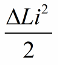
Després d'un quart del període, el condensador comença a descarregar-se, la seva energia es torna a convertir en l'energia del camp magnètic de la bobina.Quan el camp magnètic assoleixi l'amplitud, tornarem a prémer el nucli amb força. De nou, la inductància va augmentar, augmentada en la mateixa quantitat.

I de nou, a corrent zero, tornem la inductància al seu valor original. Com a resultat, si els guanys d'energia per a cada mig cicle superen les pèrdues de resistència, l'energia del bucle augmentarà tot el temps i augmentarà l'amplitud de l'oscil·lació. Aquesta situació s'expressa per la desigualtat:

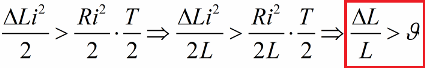
Aquí vam dividir ambdós costats d'aquesta desigualtat per L i vam escriure la condició per a la possibilitat d'excitació paramètrica per salts per a un cert valor del decrement logarítmic.

Es recomana canviar la inductància (o la capacitat) dues vegades per període, per tant, la freqüència del canvi de paràmetre (freqüència de ressonància paramètrica) hauria de ser el doble de la freqüència natural del sistema oscil·lant:

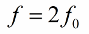
Així, el camí d'excitació de les oscil·lacions en el circuit ha aparegut sense necessitat de canviar directament l'EMF o el corrent.El corrent fluctuant inicial en el circuit sempre està present d'una manera o altra, i això ni tan sols té en compte les interferències de les oscil·lacions de radiofreqüència a l'atmosfera.

Si la inductància (o la capacitat) no canvia en els salts, però harmònicament, la condició per a l'ocurrència d'oscil·lacions serà una mica diferent:

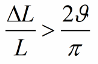
Com que la capacitat i la inductància són paràmetres del circuit (com la massa d'un pèndol o l'elasticitat d'una molla), el mètode d'excitació d'oscil·lacions també s'anomena excitació paramètrica.

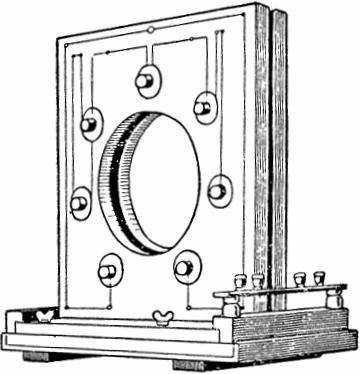
Aquest fenomen va ser descobert i estudiat pràcticament a principis del segle XX pels físics soviètics Mandelstam i Papalexi. A partir d'aquest fenomen físic, van construir el primer generador de CA paramètric amb una potència de 4 kW i inductància variable.

En el disseny del generador, es van situar set parells de bobines planes a banda i banda del marc, a la cavitat de les quals girava un disc ferromagnètic amb sortints. Quan el disc és impulsat per girar per un motor, les seves protuberàncies es mouen periòdicament dins i fora de l'espai entre cada parell de bobines, canviant així la inductància i excitant les oscil·lacions.