Procés oscil·latori en enginyeria elèctrica i electrònica, tipus d'oscil·lacions
Procés oscil·latori: un procés amb diferents graus de repetibilitat. Tots els processos oscil·latoris es divideixen en 2 classes: periòdics i no periòdics. En teoria, també utilitzen una classe intermèdia: oscil·lacions gairebé periòdiques.
Un procés oscil·latori s'anomena periòdic, en el qual el valor que caracteritza aquest procés, pres en qualsevol moment, després d'un determinat període de temps T té el mateix valor.
La funció f (t), que és una expressió matemàtica del procés oscil·latori, s'anomena periòdica amb període T si compleix la condició f (t + T) = f (t).
Entre la classe de processos oscil·latoris periòdics, el paper principal el juguen les oscil·lacions harmòniques o sinusoïdals, en les quals es produeix un canvi en una magnitud física amb el temps segons la llei del sinus o del cosinus. El seu rècord global és:
y = f (t) = aCos ((2π / T) t — φ),
on a — amplitud de les oscil·lacions, φ és la fase d'oscil·lació, 1 /T = f — freqüència i 2πf = ω — freqüència de vibracions cícliques o circulars.
Aplicació de les oscil·lacions sinusoïdals i les seves característiques:
Maneres gràfiques de mostrar el corrent altern
Una funció gairebé periòdica corresponent a una lectura d'oscil·lacions periòdiques es defineix per la condició:
| f · (t + τ) — f (t) | <= ε on ε — assigneu un valor a cada valor T.
La quantitat τ en aquest cas s'anomena gairebé període. Si el valor ε és molt petit en comparació amb el valor mitjà de f (t) en el temps T, aleshores la funció quasi periòdica serà propera a la periòdica.
Les oscil·lacions no periòdiques són molt més variades que les periòdiques. Però la majoria de vegades en l'automatització s'ha de complir amb l'amortiment o l'augment d'oscil·lacions sinusoïdals.
Les oscil·lacions segons la llei de la sinusoide amortida o, com de vegades s'anomenen, oscil·lacions harmòniques amortides, es poden representar en una forma general:
x = Ae-δTcos·(ω + φ),
on t és el temps, A i φ són constants arbitràries. La notació general de la llei de les oscil·lacions harmòniques creixents només difereix en el signe del factor d'amortiment δ[1 segon].
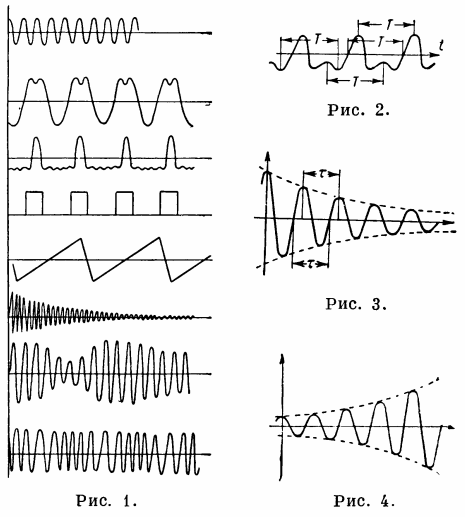
Fig. 1 — procés oscil·lant, Fig. 2. — procés periòdic, fig. 3. — oscil·lacions harmòniques en decadència, fig. 4. — augment de les oscil·lacions harmòniques.
Un exemple d'aplicació del procés oscil·latori és el circuit oscil·latori més senzill.
Circuit oscil·lador (circuit elèctric): un circuit elèctric passiu en el qual es poden produir oscil·lacions elèctriques amb una freqüència determinada pels paràmetres del propi circuit.
El circuit oscil·lant més senzill està format per la capacitat C i la inductància L. En absència d'influència externa, amortiment d'oscil·lacions amb freqüència εО = 1/2π√LC.
L'amplitud de les vibracions disminueix amb, per exemple, δT, on δ és el coeficient d'amortiment. Si δ> = eO, aleshores les oscil·lacions esmorteïdes del circuit es tornen no periòdiques.
En electrònica, la qualitat del circuit oscil·lant ve determinada pel factor de qualitat: Q = nf/δ... Quan una força periòdica externa actua sobre el circuit oscil·lant, en ell es produeixen oscil·lacions forçades. L'amplitud de les oscil·lacions forçades augmenta significativament per als circuits d'alta Q si la freqüència de la influència externa és propera a eo (ressonància). El circuit oscil·lant és una de les parts principals dels amplificadors de ressonància, generadors i altres dispositius electrònics.
Veure també sobre aquest tema: Aplicació de la ressonància de tensió i la ressonància de corrent
