Fonts d'harmònics en xarxes elèctriques

Com que els elements no lineals estan invariablement presents a l'electricitat moderna, especialment a les xarxes industrials, com a resultat, les corbes de corrent i les corbes de tensió estan distorsionades, els harmònics més alts apareixen a les xarxes.

En primer lloc, la no-sinusoïdalitat es deu a la presència de convertidors estàtics, després: generadors síncrons, màquines de soldadura, làmpades fluorescents, forns d'arc, transformadors, motors i altres càrregues no lineals.

Matemàticament, la no-sinusoïdalitat de les corbes de corrent i tensió es pot representar com la suma de l'harmònic principal de la freqüència de la xarxa i els seus harmònics superiors que són múltiples d'aquesta. L'anàlisi harmònic dóna com a resultat una sèrie de Fourier trigonomètrica, i els valors de les freqüències i les fases dels harmònics resultants es poden calcular fàcilment mitjançant la fórmula:

De fet, la combinació resultant de tensions i corrents no sinusoïdals en una xarxa trifàsica pot ser asimètrica o simètrica.Un sistema simètric de tensions no sinusoïdals per a múltiples de tres harmònics (k = 3n) condueix a la formació d'un sistema de tensions de seqüència zero.

A més, a k = 3n + 1, l'harmònic de la xarxa trifàsica genera un sistema simètric de tensions de seqüència negativa. Així, cada k-harmònica d'un sistema simètric de tensions no sinusoïdals dóna lloc a un sistema simètric de tensions de fase de seqüència directa, inversa o zero.

A la pràctica, però, el sistema de tensions de fase no sinusoïdals resulta ser asimètric. Tan, nuclis magnètics de transformadors trifàsics ells mateixos, són no lineals i asimètrics, ja que les longituds dels camins magnètics per a les fases mitja i final difereixen en un factor d'1,9. Com a resultat, els valors efectius dels corrents de magnetització de la fase mitjana són 1,3 - 1,55 vegades més petits que els valors dels corrents de magnetització de les fases finals.

Els harmònics asimètrics es descomponen en components simètrics quan cada k -harmònic forma un sistema asimètric de tensions de fase i normalment conté components de tres seqüències: zero, directe i invers.

Les xarxes trifàsiques amb neutre aïllat es caracteritzen per l'absència de components de seqüència zero en cadascuna de les fases, sempre que no hi hagi fallades a terra. Com a resultat, no hi ha múltiples de tres harmònics en els corrents de fase, però hi ha altres harmònics que contenen components de seqüència inversa i positiva.

Els rectificadors de potència, per regla general, al costat de corrent continu tenen grans inductàncies, que són bobinatges de màquina de corrent continu i reactors de suavització.Aquestes inductàncies són moltes vegades superiors a la inductància equivalent del costat de corrent altern, per tant, aquests rectificadors respecte a la xarxa de corrent altern es comporten com a fonts de corrent harmònic superior. El corrent dirigit a la xarxa amb una freqüència harmònica té un valor que no depèn dels paràmetres de la xarxa de subministrament.

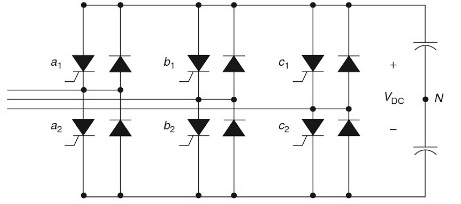
Per a xarxes elèctriques trifàsiques, és característic utilitzar rectificadors trifàsics d'ona completa per a 6 vàlvules com a tals convertidors, dels quals s'anomenen de sis polsos o sisfàsics. La corba de corrent per a cadascuna de les fases en aquest cas es pot descriure per l'equació (per al corrent d'una fase A):

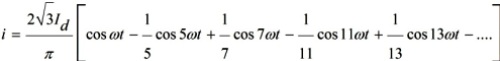
Es pot veure que els corrents de fase només contenen harmònics senars que no són múltiples de tres, i els signes d'aquests harmònics s'alternen: harmònics positius de l'ordre 6k + 1r i harmònics negatius de l'ordre 6k-1r.

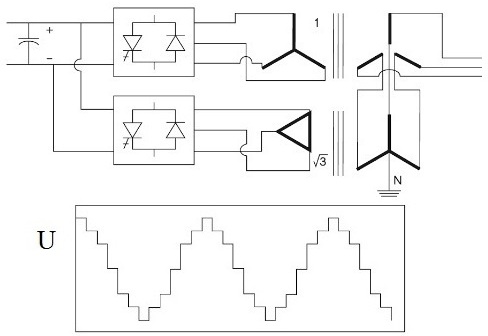
Si s'utilitza un rectificador de dotze fases, quan un parell de rectificadors de sis fases es connecta a un parell de transformadors trifàsics (les tensions secundàries es desfasen per pi / 6), aleshores els harmònics de 12k + 1 i 12k- Apareixeran 1-ordres, respectivament.

Abans d'utilitzar els rectificadors, només els transformadors i diverses màquines elèctriques eren la principal font d'harmònics superiors a les xarxes elèctriques. Però encara avui els transformadors són els elements més comuns de les xarxes elèctriques.

La raó per la qual els transformadors generen harmònics més alts és la corba de magnetització no lineal dels circuits magnètics i la presència constant de bucles d'histèresi… Una corba de magnetització no lineal i un bucle d'histèresi generen distorsions del corrent de magnetització sense càrrega sinusoïdal original i el resultat són harmònics més alts en el corrent que el transformador extreu de la xarxa.

Els transformadors de la classe 110 kV no tenen més de l'1% de corrent sense càrrega i els transformadors de la classe 6-10 kV, no més del 2-3%. Són corrents petites i les seves pèrdues actives en el circuit magnètic són insignificants. És la corba de magnetització la que importa, no el bucle d'histèresi.

La corba de magnetització és simètrica i ni tan sols hi ha harmònics en l'expansió de la sèrie de Fourier. La distorsió del corrent de magnetització és causada per harmònics senars, entre els quals hi ha múltiples de tres. El tercer harmònic és especialment pronunciat, però els harmònics cinquè i setè també són els més significatius.

Els harmònics EMF i els harmònics de corrent també són característics dels motors, tant sincrònics com asíncrons… Aquests harmònics són causats pels mateixos fenòmens que els harmònics actuals generats pels transformadors: la no linealitat de la corba de magnetització dels materials dels quals estan fets l'estator i el rotor.

L'espectre de freqüències dels harmònics actuals dels motors elèctrics, com el dels transformadors, inclou els harmònics senars, entre els quals òbviament hi ha múltiples de tres. Els més significatius aquí són els harmònics 3r, 5è i 7è.

Com en el cas dels transformadors, els càlculs aproximats ens permeten prendre el percentatge de corrents del 3r, 5è i 7è harmònic en un 40% per al tercer harmònic, un 30% per al cinquè harmònic i un 20% per al setè harmònic (percentatge de el corrent inactiu).