Càlculs de circuits magnètics

A les màquines i aparells elèctrics, el flux magnètic F es concentra al circuit magnètic (nucli ferromagnètic) i als entrefers d'aquest circuit magnètic. Aquest camí de flux magnètic s'anomena circuit magnètic.

Un circuit magnètic és com un circuit elèctric. El flux magnètic Ф s'assembla a un corrent elèctric I, la inducció В s'assembla a una densitat de corrent, la força magnetitzant (ns) Fн (H ∙ l = I ∙ ω) correspon a e. etc. amb

En el cas més senzill, el circuit magnètic té la mateixa secció transversal a tot arreu i està fet d'un material magnètic homogeni. Per determinar n. amb l ∙ ω necessària per proporcionar la inducció requerida B, la intensitat corresponent H es determina a partir de la corba de magnetització i es multiplica per la longitud mitjana de la línia de camp magnètic l: H ∙ l = I ∙ ω = Fm.

A partir d'aquí, es determina el corrent requerit I o el nombre de voltes ω de la bobina.

Un circuit magnètic complex sol tenir seccions amb diferents seccions i materials magnètics. Aquests trams solen estar connectats en sèrie, per tant el mateix flux magnètic F passa per cadascun d'ells.La inducció B a cada secció depèn de la secció transversal de la secció i es calcula per a cada secció per separat mitjançant la fórmula B = Φ∶S.

Per a diferents valors d'inducció, la intensitat H es determina a partir de la corba de magnetització i es multiplica per la longitud mitjana de la línia elèctrica de la secció corresponent del circuit. Resumint les obres individuals, s'obté la n completa. c. circuit magnètic:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … que determina el corrent de magnetització o el nombre de voltes de la bobina.

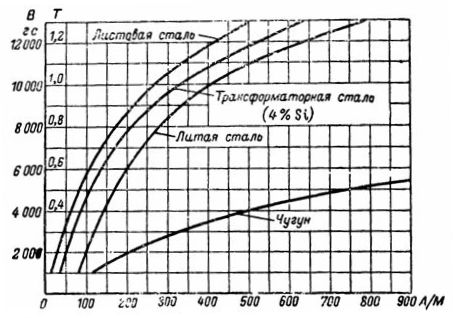
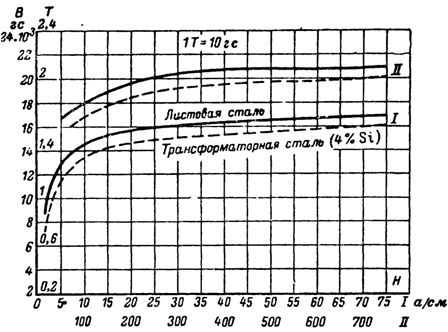
Corbes de magnetització

Exemples de

1. Quin ha de ser el corrent de magnetització I d'una bobina de 200 espires perquè n. c) va crear a l'anell de ferro colat un flux magnètic Ф = 15700 Ms = 0,000157 Wb? El radi mitjà de l'anell de ferro colat és r = 5 cm, i el diàmetre de la seva secció és d = 2 cm (Fig. 1).

Arròs. 1.

Secció del circuit magnètic S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

La inducció al nucli és: B = Φ∶S = 15700∶3,14 = 5000 G.

En el sistema MKSA, la inducció és: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

A partir de la corba de magnetització del ferro colat, trobem la força requerida H igual a 750 A/m per a B = 5000 G = 0,5 T. La força de magnetització és igual a: I ∙ ω = H ∙ l = 235,5 Av.

Per tant, el corrent requerit I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Un circuit magnètic tancat (Fig. 2) està fet de plaques d'acer d'un transformador. Quantes voltes hi ha d'haver en una bobina amb un corrent de 0,5 A per crear un flux magnètic al nucli Ф = 160000 Ms = 0,0016 Wb?

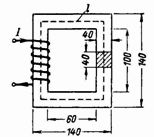
Arròs. 2.

Secció del nucli S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Inducció del nucli B = F / S = 160000/16 = 10000 Gs = 1 T.

Segons la corba de magnetització de l'acer del transformador, trobem per a B = 10.000 Gs = 1 T la intensitat H = 3,25 A / cm = 325 A / m.

La longitud mitjana de la línia del camp magnètic és l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Força magnetitzant Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Av.

Amb un corrent de 0,5 A, el nombre de voltes és ω = 156 / 0,5 = 312.

3. El circuit magnètic que es mostra a la fig. 3 és similar al circuit magnètic de l'exemple anterior, excepte que té un entrefer de δ = 5 mm. Què hauria de ser. s. i el corrent de la bobina de manera que el flux magnètic sigui el mateix que en l'exemple anterior, és a dir, F = 160000 Ms = 0,0016 Wb?

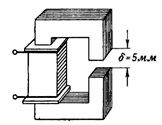
Arròs. 3.

El circuit magnètic té dues seccions connectades en sèrie, la secció transversal de les quals és la mateixa que en l'exemple anterior, és a dir, S = 16 cm2. La inductància també és igual a B = 10000 G = 1 T.

La longitud mitjana de la línia magnètica d'acer és lleugerament més curta: lс = 48-0,5 = 47,5 cm ≈0,48 m.

La tensió magnètica en aquesta secció del circuit magnètic és Hc ∙ lc = 3,25 ∙ 48≈156 Av.

La força de camp a l'entrefer és: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A / cm.

La tensió magnètica a la secció transversal de l'entrefer Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Completa n. c. és igual a la suma de les tensions magnètiques en seccions individuals: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13,3 A.

Si en l'exemple anterior el flux magnètic requerit era proporcionat per un corrent de 0,5 A, llavors per a un circuit magnètic amb un entrefer de 0,5 cm es necessita un corrent de 13 A per obtenir el mateix flux magnètic. D'això es pot veure que un entrefer, fins i tot insignificant en relació a la longitud del circuit magnètic, augmenta molt el n requerit. v. i corrent de bobina.

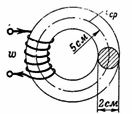
4. Es calcula que el flux magnètic del transformador és F = 72000 Ms. Cal el càlcul de n.s.i corrent magnetitzant del bobinatge primari que té 800 espires. Hi ha un buit δ = 0,2 mm al nucli del transformador. Les dimensions del nucli del transformador es mostren a la fig. 4. Secció transversal del nucli S = 2 ∙ 3 ​​​​​​= 6 cm2 (els transformadors amb nuclis d'aquesta forma s'anomenen blindats).

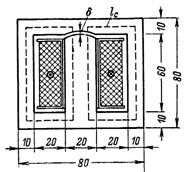
Arròs. 4.

Inducció de nucli i entrefer B = F / S = 72000/6 = 12000 G.

Segons la corba de magnetització de l'acer del transformador per a B = 12000 G, determinem la intensitat: Hc = 5 A / cm.

La longitud mitjana de la línia magnètica en acer és lс = 2 ∙ (6 + 3) = 18 cm.

Tensió a l'entrefer Hδ = 0,8 ∙ B = 9600 A / cm.

Força magnetitzant I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0,35 A.

Al nucli blindat, el flux magnètic es divideix en dues parts, que es tanquen al llarg de les barres laterals, la secció transversal de les quals és S / 2 i la longitud mitjana de la línia magnètica és lc. Com a resultat, el circuit magnètic és completament anàleg al circuit magnètic d'un transformador convencional amb un nucli comú S i una longitud de la línia elèctrica lc.

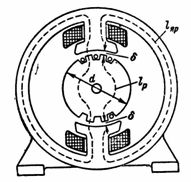
5. El flux magnètic de la màquina de corrent continu F = 1280000 Mks. El circuit magnètic conté un jou d'acer fos amb una longitud mitjana de línia magnètica lа = 80 cm, un rotor muntat a partir de plaques d'acer elèctric amb una longitud de camp mitjana lр = 18 cm i dos espais d'aire δ 0,2 cm cadascun. = 8 ∙ 20 cm2; rotor i secció polar Sр = 12 ∙ 20 cm2... Calcula n. p.i el nombre de voltes de la bobina del pol, si el màxim de corrent magnetitzant (excitant) en ella és d'1 A (Fig. 5).

Arròs. 5.

Inducció al jou i al pol Bя = Ф / Sя = 1280000/160 = 8000 G.

La tensió al jou i al pol segons la corba de magnetització de l'acer fos a Bя = 8000 G és igual a:

H = 2,8 A/cm.

La força de magnetització a la secció del jou HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Inducció al rotor, pol i entrefer Br = Ф / Ср = 1280000/240 = 5333 G.

Tensió en un rotor fet de plaques d'acer a Br = 5333 Gs Hrp = 0,9 A / cm,

i la tensió magnètica de la secció del rotor Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Tensió a l'entrefer Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A / cm.

La tensió magnètica a la secció transversal de l'entrefer Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Completa n. c) igual a la suma de tensions magnètiques en seccions separades: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Av.

El nombre de voltes de les bobines de dos pols ω = (I ∙ ω) / I = 1946,76 / 1≈2000.