Teoria dels autòmats, autòmats finits
L'estructura, el disseny i el principi de funcionament de diverses màquines estan determinats en gran mesura pel seu propòsit funcional. Distingir entre màquines tecnològiques, de transport, informàtiques, militars i altres. Complexos automàtics sencers dissenyats per realitzar processos tecnològics complexos s'introdueixen àmpliament en diverses indústries. Es dissenyen i construeixen autòmats que realitzen diverses funcions lògiques (màquines lògiques).
Teoria dels autòmats — secció de cibernètica, que va sorgir sota la influència dels requisits de la tecnologia dels ordinadors digitals i les màquines de control. Els autòmats discrets estudiats en la teoria d'autòmats són models abstractes de sistemes reals (tant tècnics com biològics) que processen informació discreta (digital) en passos de temps discrets.
La teoria dels autòmats es basa en conceptes matemàtics precisos que formalitzen idees intuïtives sobre el funcionament (comportament) de l'autòmat i sobre la seva estructura (estructura interna).
En aquest cas, la transformació d'informació s'entén sempre com una operació que transforma seqüències d'entrada compostes per lletres de l'alfabet d'entrada en seqüències de sortida compostes per lletres de l'alfabet de sortida.
S'utilitza àmpliament l'aparell de lògica matemàtica, àlgebra, teoria de probabilitats, combinatòria i teoria de grafs.
El problema amb la teoria dels autòmats en algunes de les seves parts (teoria estructural dels autòmats) va créixer de la teoria dels circuits de relé-contacte, que va començar a prendre forma a finals dels anys trenta. inclusiu mètodes d'àlgebra lògica.

En la teoria estructural dels autòmats s'estudien diferents tipus d'esquemes, dissenyats per descriure com es crea un autòmat complex a partir de components (elements) més simples connectats correctament en un sistema.
Una altra direcció, anomenada teoria abstracta dels autòmats, estudia el comportament dels autòmats (és a dir, la naturalesa de la transformació de la informació que duen a terme), tot abstraint-se de les especificitats de la seva estructura interna, i va sorgir a la dècada de 1950.
En el marc de la teoria abstracta dels autòmats, el contingut dels conceptes "autòmat" i "màquina" s'esgota essencialment per la descripció estàndard de la transformació de la informació que duu a terme un autòmat. Aquesta transformació pot ser determinista, però també pot ser de naturalesa probabilística.
Les més estudiades són les màquines deterministes (autòmats), que inclouen autòmats finits, el principal objecte d'estudi de la teoria dels autòmats.
Una màquina d'estats finits es caracteritza per una quantitat limitada de memòria (el nombre d'estats interns) i es defineix mitjançant una funció de transició.Amb una idealització raonable, totes les màquines matemàtiques modernes i fins i tot el cervell, des del punt de vista del seu funcionament, es poden considerar autòmats finits.
Els termes "màquina seqüencial", "autòmat Milly", "autòmat Moore" s'utilitzen a la literatura (i no de manera uniforme per tots els autors) com a sinònims del terme "autòmat finit" o per emfatitzar certes característiques en les funcions de transició d'un finit. autòmat.
Els autòmats amb memòria il·limitada són una màquina de Turing capaç de realitzar (potencialment) qualsevol transformació eficient de la informació. El concepte de "màquina de Turing" va sorgir abans que el concepte de "màquina d'estats finits" i s'estudia principalment en la teoria dels algorismes.
La teoria abstracta dels autòmats està estretament relacionada amb les teories algebraiques conegudes, per exemple la teoria de semigrups. Des d'un punt de vista aplicat, són interessants els resultats que caracteritzen la transformació de la informació en un autòmat pel que fa a la mida de la memòria.
És el cas, per exemple, en problemes amb experiments amb autòmats (treballs d'E.F. Moore, etc.), on una o altra informació sobre les funcions de transició de l'autòmat o sobre la capacitat de la seva memòria s'obté a partir dels resultats de la experiments.
Una altra tasca és calcular els períodes de les seqüències de sortida, a partir de la informació disponible sobre la mida de memòria de l'autòmat i els períodes de les seqüències d'entrada.
És de gran importància el desenvolupament de mètodes per minimitzar la memòria de les màquines d'estats finits i estudiar el seu comportament en entorns aleatoris.
En la teoria abstracta d'autòmats, el problema de síntesi és el següent.Pel que fa a un llenguatge clarament formalitzat, s'escriuen les condicions per al comportament de l'autòmat dissenyat (per a l'esdeveniment representat a l'autòmat). En aquest cas, cal desenvolupar mètodes que segons cada condició escrita:
1) esbrinar si existeix una màquina d'estats que la informació transformada compleixi aquesta condició;
2) si és així, llavors es construeixen les funcions de transició d'aquesta màquina d'estats finits o s'estima la seva mida de memòria.
La solució de la tasca de síntesi en aquesta formulació pressuposa la creació preliminar d'un llenguatge convenient per registrar les condicions de funcionament d'un autòmat amb algorismes convenients per a la transició de l'enregistrament a les funcions transitives.
En la teoria estructural dels autòmats, el problema de síntesi consisteix a construir una cadena d'elements d'un tipus determinat que realitza un autòmat finit donat per les seves funcions de transició. En aquest cas, solen enunciar algun criteri d'optimitat (per exemple, el nombre mínim d'elements) i busquen obtenir un esquema òptim.
Com es va veure més tard, això significa que alguns dels mètodes i conceptes desenvolupats anteriorment en relació als circuits de contacte de relé són aplicables a circuits d'un altre tipus.
En relació amb el desenvolupament de les tecnologies electròniques, els més estesos són els esquemes d'elements funcionals (xarxes lògiques). Un cas especial de xarxes lògiques són les xarxes neuronals abstractes, els elements de les quals s'anomenen neurones.
S'han desenvolupat molts mètodes de síntesi, depenent del tipus de circuits i de la transformació de la informació a què estan destinats (Síntesi de dispositius de relé).
Mira -Minimització de circuits combinacionals, mapes de Carnot, síntesi de circuits
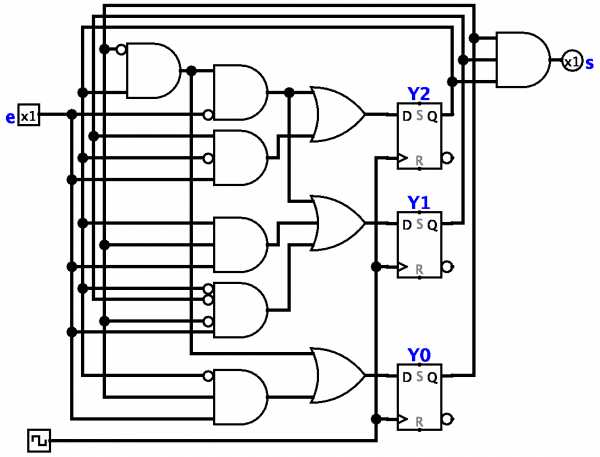
Màquina d'estats finits — un model matemàtic d'un sistema de control amb una mida de memòria fixa (incapaç d'augmentar durant el funcionament).
El concepte de màquina d'estats finits és una abstracció matemàtica que caracteritza les característiques generals d'un conjunt de sistemes de control (per exemple, un dispositiu de relé de múltiples bucles). Tots aquests sistemes tenen característiques comunes que és natural acceptar com a definició d'autòmat finit.
Cada autòmat acabat té una entrada exposada a influències externes i elements interns. Tant per als elements d'entrada com per als elements interns, hi ha un nombre fix d'estats discrets que poden prendre.
El canvi en els estats dels elements d'entrada i interns es produeix en moments discrets en el temps, els intervals entre els quals s'anomenen ticks. L'estat intern (l'estat dels elements interns) al final de la cinta està determinat completament per l'estat intern i l'estat de l'entrada al començament de la cinta.
Totes les altres definicions d'autòmat finit es poden reduir a aquesta característica, en particular definicions que suposen que un autòmat finit té una sortida que depèn de l'estat intern de l'autòmat en un moment donat.
En termes d'aquesta característica, la naturalesa de les seves entrades i estats interns és irrellevant per a la descripció d'un autòmat complet. En lloc d'entrades i estats, només podeu mirar els seus números amb una numeració aleatòria.
La màquina d'estat s'establirà si s'especifica la dependència del seu número d'estat intern del número d'estat intern anterior i del número d'estat d'entrada anterior. Aquesta tasca pot ser en forma de taula final.
Una altra manera habitual de definir un autòmat complet és la construcció de l'anomenat diagrames de transició. Els estats d'entrada sovint s'anomenen simplement entrades, i els estats interns són simplement estats.
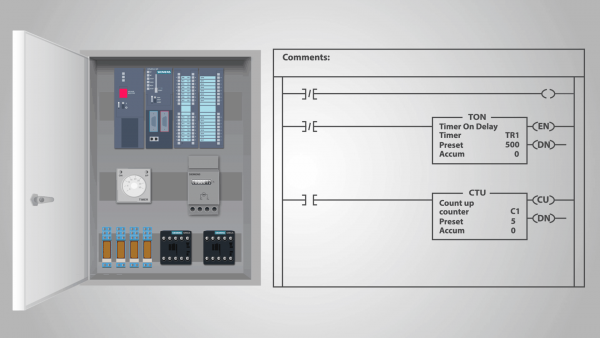
Una màquina d'estats finits pot ser un model tant de dispositius tècnics com d'alguns sistemes biològics. Els autòmats del primer tipus són, per exemple, dispositius de relé i diversos ordinadors electrònics, incl. controladors lògics programables.
En el cas d'un dispositiu de relé, el paper dels estats d'entrada el juguen les combinacions d'estats dels elements sensibles del dispositiu de relé (cada combinació d'aquests estats és un «estat complex», caracteritzat per una indicació de tots els elements sensibles de aquests estats discrets que tenen en un moment determinat). De la mateixa manera, les combinacions d'estats d'elements intermedis d'un dispositiu de relé actuen com a estats interns.
Un controlador lògic programable (PLC) és un exemple de dispositiu d'acció de relé que es pot anomenar màquina d'estat autònoma.
De fet, un cop el programa s'ha introduït al PLC i el controlador ha començat a calcular, no està exposat a influències externes i cada estat posterior està completament determinat pel seu estat anterior. Podem suposar que l'entrada té el mateix estat en cada cicle de rellotge.
Per contra, qualsevol màquina d'estats finits que tingui l'únic estat d'entrada possible s'anomena naturalment autònoma, ja que en aquest cas l'entorn extern no porta informació que controli el seu comportament.
Vegeu també:
L'ús de sistemes de microprocessadors en enginyeria elèctrica sobre l'exemple de l'ús de PLC