Què és un subministrament elèctric?

L'home modern es troba constantment amb l'electricitat a la vida quotidiana i a la feina, utilitza aparells que consumeixen corrent elèctric i aparells que el generen. Quan treballeu amb ells, sempre heu de tenir en compte les seves capacitats inherents a les característiques tècniques.

Un dels principals indicadors de qualsevol aparell elèctric és una magnitud tan física com l'energia elèctrica... És habitual anomenar intensitat o velocitat de generació, transmissió o conversió de l'electricitat en altres tipus d'energia, per exemple, calor, llum, etc. mecànica.

El transport o transferència de gran energia elèctrica amb finalitats industrials es realitza segons línies elèctriques d'alta tensió.

Transformació energia elèctrica es realitza a les subestacions transformadores.

El consum d'electricitat es produeix en dispositius domèstics i industrials amb diferents finalitats. Un dels seus tipus comuns són làmpades incandescents de diferents graus.

La potència elèctrica dels generadors, línies elèctriques i consumidors en circuits de CC i CA té el mateix significat físic, que s'expressa simultàniament en diferents proporcions en funció de la forma dels senyals compostos. Per definir els patrons generals, les nocions de valors instantanis... Tornen a destacar la dependència de la velocitat de transformació de l'electricitat en el temps.

Determinació de la potència elèctrica instantània

En l'enginyeria elèctrica teòrica, per tal de derivar les relacions bàsiques entre corrent, voltatge i potència, s'utilitzen les seves imatges en forma de valors instantanis, que es fixen en un moment determinat del temps.

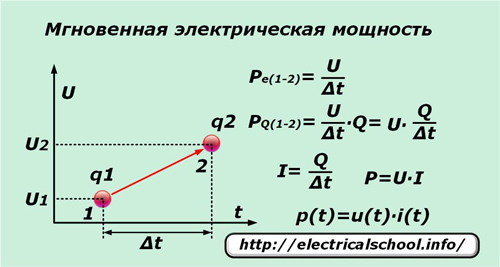
Si en un període de temps molt curt ∆t una única càrrega elemental q sota la influència de la tensió U es mou del punt «1» al punt «2», aleshores realitza un treball igual a la diferència de potencial entre aquests punts. Dividint-ho per l'interval de temps ∆t, obtenim l'expressió de la potència instantània per unitat de càrrega Pe (1-2).

Com que no només la càrrega única es mou sota l'acció de la tensió aplicada, sinó també totes les adjacents que estan sota la influència d'aquesta força, el nombre de la qual es representa convenientment pel nombre Q, llavors el valor instantani de la potència PQ (1-2) es pot escriure per a ells.

Després de realitzar transformacions senzilles, obtenim l'expressió de la potència P i la dependència del seu valor instantani p (t) dels components del producte del corrent instantani i (t) i la tensió u (t).

Determinació de la potència elèctrica constant

V Circuits de corrent continu la magnitud de la caiguda de tensió a la secció del circuit i el corrent que hi circula no canvia i es manté estable, igual als valors instantanis.Per tant, la potència en aquest circuit es pot determinar multiplicant aquests valors o dividint l'obra perfecta A pel període de la seva execució, tal com es mostra a la imatge explicativa.

Determinació de la potència elèctrica de corrent altern

Les lleis de variació sinusoïdal de corrents i voltatges transmesos a través de xarxes elèctriques imposen la seva influència en l'expressió de potència en aquests circuits. Aquí entra en joc la potència aparent, que es descriu pel triangle de potència i consta de components actius i reactius.

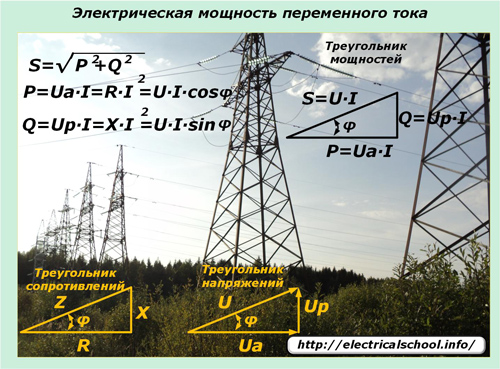
Un corrent elèctric sinusoïdal en passar per línies elèctriques amb diferents tipus de càrregues en totes les seccions no canvia la forma del seu harmònic i la caiguda de tensió a les càrregues reactives es desplaça en fase en una determinada direcció. Les expressions de valor de moment ajuden a comprendre l'efecte de les càrregues aplicades sobre el canvi de potència en el circuit i la seva direcció.

Al mateix temps, presteu atenció immediatament al fet que la direcció del flux de corrent des del generador fins al consumidor i la potència transmesa a través del circuit creat són coses completament diferents, que en alguns casos poden no només no coincidir, sinó que també seran. dirigit en direccions oposades.

Considereu aquestes relacions en la seva manifestació ideal i pura per a diferents tipus de càrregues:

• actiu;

• capacitiu;

• inductiu.

Dissipació de potència de càrrega activa

Suposarem que el generador produeix una tensió sinusoïdal ideal u que s'aplica a la resistència purament activa del circuit. L'amperímetre A i el voltímetre V mesuren el corrent I i la tensió U cada vegada que t.

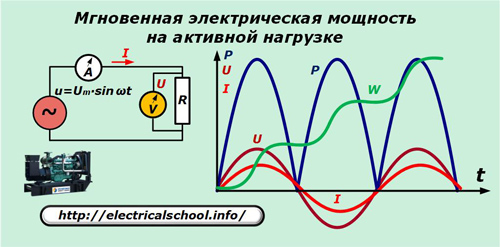
El gràfic mostra que els sinusoides del corrent i la caiguda de tensió a través de la resistència activa coincideixen en freqüència i fase, fent les mateixes oscil·lacions. La força expressada pel seu producte oscil·la al doble de la freqüència i sempre roman positiva.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Si anem a l'expressió tensió de funcionament, aleshores obtenim: p = P ∙ (1-cos2ωt).

A continuació, integrarem la potència durant el període d'una oscil·lació T i podrem notar que el guany d'energia ∆W durant aquest interval augmenta. Amb el temps, la resistència continua consumint noves porcions d'electricitat, tal com es mostra al gràfic.

Amb càrregues reactives, les característiques del consum d'energia són diferents, tenen una forma diferent.

Dissipació de potència capacitiva

Al circuit elèctric del generador, substituïu l'element resistiu per un condensador de capacitat C.

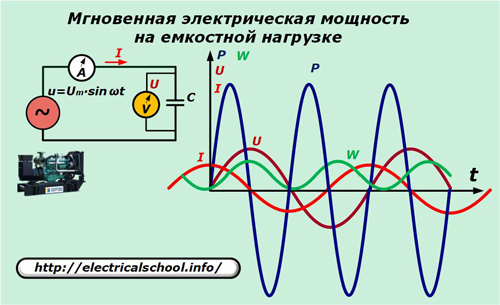
La relació entre el corrent i la caiguda de tensió de la capacitat s'expressa amb la relació: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Multipliquem els valors de les expressions instantànies de corrent per tensió i obtenim el valor de la potència que consumeix la càrrega capacitiva.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° sin2 C)ωt

Aquí podeu veure que la potència oscil·la al voltant de zero al doble de la freqüència de la tensió aplicada. El seu valor total per al període harmònic, així com el guany d'energia, és zero.

Això vol dir que l'energia es mou al llarg del circuit tancat del circuit en ambdues direccions, però no funciona.Aquest fet s'explica pel fet que quan la tensió de la font augmenta en valor absolut, la potència és positiva i el flux d'energia a través del circuit es dirigeix ​​al contenidor, on s'acumula energia.

Després que la tensió passa a la secció harmònica caiguda, l'energia es retorna del condensador al circuit a la font. No es fa cap treball útil en cap dels dos processos.

Potència dissipada en una càrrega inductiva

Ara, al circuit d'alimentació, substituïu el condensador per la inductància L.

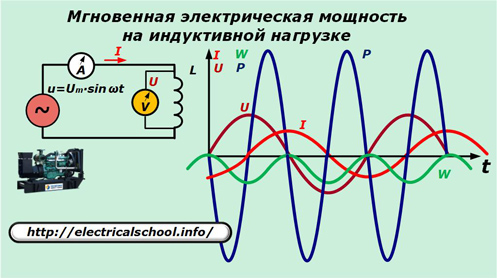
Aquí el corrent a través de la inductància s'expressa per la relació:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Aleshores aconseguim

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL2)

Les expressions resultants ens permeten veure la naturalesa del canvi en la direcció de la potència i l'augment d'energia sobre la inductància, que realitzen les mateixes oscil·lacions que no serveixen per fer treball, com sobre la capacitat.

La potència alliberada en càrregues reactives s'anomena component reactiu. En condicions ideals, quan els cables de connexió no tenen resistència activa, sembla inofensiu i no causa cap dany. Però en condicions de potència real, els transitoris periòdics i les fluctuacions de la potència reactiva provoquen l'escalfament de tots els elements actius, inclosos els cables de connexió, per als quals es consumeix una mica d'energia i el valor de la potència total aplicada de la font disminueix.

La principal diferència entre el component reactiu de la potència és que no realitza cap treball útil, però provoca pèrdues d'energia elèctrica i excés de càrregues en els equips, que són especialment perillosos en situacions crítiques.

Per aquests motius, per eliminar la influència de la potència reactiva, esp sistemes tècnics per a la seva compensació.

Distribució de potència a càrrega mixta

Com a exemple, utilitzem la càrrega d'un generador amb una característica capacitiva activa.

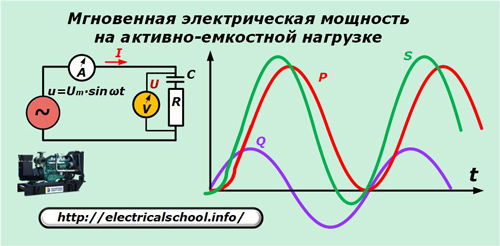
Per simplificar la imatge, els sinusoides de corrents i voltatges no es mostren al gràfic donat, però cal tenir en compte que amb una naturalesa activa-capacitiva de la càrrega, el vector de corrent condueix la tensió.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Després de les transformacions obtenim: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Aquests dos termes de l'última expressió són els components actius i reactius de la potència aparent instantània. Només el primer d'ells fa un treball útil.

Eines de mesura de potència

Per analitzar el consum d'electricitat i calcular-lo, s'utilitzen aparells de mesura, que des de fa temps s'han anomenat «Comptadors»… El seu treball es basa en mesurar els valors efectius de corrent i tensió i multiplicar-los automàticament amb una sortida d'informació.

Els comptadors mostren el consum d'energia comptant el temps de funcionament dels aparells elèctrics de manera incremental des del moment en què el comptador s'encén sota càrrega.

Per mesurar el component actiu de la potència en circuits de CA, wattmetres, i reactiu - varmetres. Tenen diferents designacions d'unitats:

• watt (W, W);

• var (var, var, var).

Per determinar el consum total d'energia, cal calcular-ne el valor mitjançant la fórmula del triangle de potència a partir de les lectures del vatímetre i el varmetre. S'expressa en les seves pròpies unitats: volt-amperes.

Les designacions acceptades de les unitats de cadascun ajuden els electricistes a jutjar no només el seu valor, sinó també la naturalesa del component de potència.