Triangles de tensions, resistències i potències

Qualsevol que tingui una idea dels diagrames vectorials notarà fàcilment que es pot distingir molt clarament un triangle de tensió en angle recte, cada costat del qual reflecteix: la tensió total del circuit, la tensió de la resistència activa i la tensió. sobre la reactància.

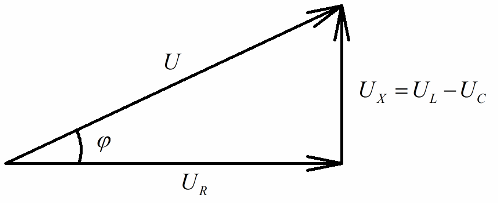
D'acord amb el teorema de Pitàgores, la relació entre aquestes tensions (entre la tensió total del circuit i la tensió de les seves seccions) serà així:

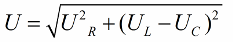
Si el següent pas és dividir els valors d'aquestes tensions pel corrent (el corrent flueix per totes les seccions del circuit en sèrie per igual), llavors per Llei d'Ohm obtenim els valors de la resistència, és a dir, ara podem parlar d'un triangle rectangle de resistències:

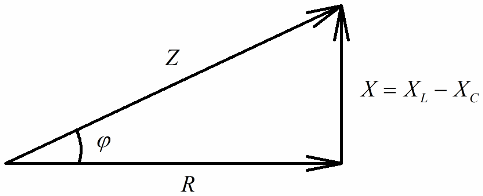
De manera similar (com en el cas de les tensions), utilitzant el teorema de Pitàgores, és possible establir una relació entre la impedància del circuit i les reactàncies. La relació s'expressarà per la fórmula següent:

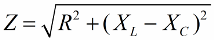
A continuació, multipliquem els valors de la resistència pel corrent, de fet augmentarem cada costat del triangle rectangle un nombre determinat de vegades. Com a resultat, obtenim un triangle rectangle amb capacitats:

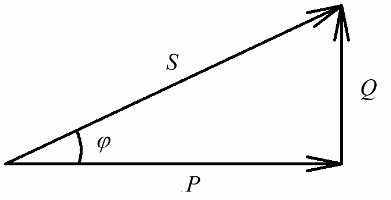
La potència activa alliberada a la resistència activa del circuit associada a la conversió irreversible d'energia elèctrica (en calor, en la realització del treball a la instal·lació) estarà clarament relacionada amb la potència reactiva implicada en la conversió reversible d'energia (la creació de camps magnètics i elèctrics en bobines i condensadors) i amb plena potència subministrada a la instal·lació elèctrica.

La potència activa es mesura en watts (W), la potència reactiva - en varis (VAR - volt-ampere reactiu), total - en VA (volt-ampere).

Segons el teorema de Pitàgores, tenim dret a escriure:

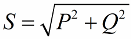
Fixem-nos ara en el fet que al triangle de potència hi ha un angle phi, el cosinus del qual és fàcil de determinar principalment per la potència activa i la potència aparent. El cosinus d'aquest angle (cos phi) anomenat factor de potència. Mostra quant de la potència total es comptabilitza quan es fa un treball útil en una instal·lació elèctrica i no es retorna a la xarxa.

Òbviament, un factor de potència més alt (màxim) indica una major eficiència de conversió de l'energia lliurada a la planta per al funcionament. Si el factor de potència és 1, tota l'energia subministrada s'utilitza per fer el treball.

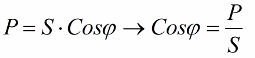
Les ràtios obtingudes permeten expressar el consum actual de la instal·lació en termes de factor de potència, potència activa i tensió de xarxa:

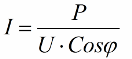
Per tant, com més petit sigui el cosinus phi, més corrent requerirà la xarxa per fer una determinada feina. A la pràctica, aquest factor (corrent de xarxa màxima) limita la capacitat de transmissió de la línia de transmissió i, per tant, com més baix és el factor de potència, més gran és la càrrega de la línia i menor és l'ample de banda útil (el baix cosinus phi condueix a la restricció). Les pèrdues en joules a les línies elèctriques amb un cosinus phi decreixent es poden veure a partir de la fórmula següent:

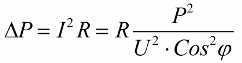
A la resistència activa R de la línia de transmissió, les pèrdues augmenten com més gran és el corrent I, tot i que és reactiu a la càrrega. Per tant, podem dir que amb un factor de potència baix, el cost de la transmissió d'electricitat simplement augmenta. Això significa que augmentar el cosinus phi és una tasca econòmica nacional important.

És desitjable que el component reactiu de la potència total s'acosti a zero, per fer-ho, seria bo fer servir sempre motors elèctrics i transformadors a plena càrrega i apagar-los al final de l'ús perquè no estiguin al ralentí. Sense càrrega, els motors i transformadors tenen un factor de potència molt baix. Una manera d'augmentar el cosinus phi als usuaris és utilitzar bancs de condensadors i compensadors síncrons.