Llei de conservació de l'energia

La física moderna coneix molts tipus d'energia associades amb el moviment o diferents disposicions mútues d'una gran varietat de cossos materials o partícules, per exemple, qualsevol cos en moviment té energia cinètica proporcional al quadrat de la seva velocitat. Aquesta energia pot canviar si la velocitat del cos augmenta o disminueix. Un cos elevat sobre el terra té una energia potencial gravitatòria que varia tres canvis en l'alçada del cos.

Les càrregues elèctriques estacionàries que es troben a certa distància les unes de les altres tenen una energia potencial electrostàtica d'acord amb el fet que, segons la llei de Coulomb, les càrregues s'atrauen (si són de signe diferent) o es repel·len amb una força inversament proporcional al quadrat de la distància entre ells.

L'energia cinètica i potencial la posseeixen les molècules, els àtoms i les partícules, els seus components: electrons, protons, neutrons, etc. en forma de treball mecànic, en el flux de corrent elèctric, en la transferència de calor, en el canvi de l'estat intern dels cossos, en la propagació d'ones electromagnètiques, etc.

Fa més de 100 anys es va establir una llei fonamental de la física, segons la qual l'energia no pot desaparèixer ni sorgir del no-res. Ella només pot canviar d'un tipus a un altre... Aquesta llei s'anomena llei de conservació de l'energia.

En els treballs d'A. Einstein, aquesta llei es desenvolupa significativament. Einstein va establir la intercanviabilitat de l'energia i la massa i, per tant, va ampliar la interpretació de la llei de conservació de l'energia, que ara s'indica habitualment com la llei de conservació de l'energia i la massa.

D'acord amb la teoria d'Einstein, qualsevol canvi en l'energia del cos dE està relacionat amb un canvi en la seva massa dm per la fórmula dE =dmc2, on c és la velocitat de la llum en el buit igual a 3 x 108 Miss.

D'aquesta fórmula, en particular, es dedueix que si, com a resultat d'algun procés, la massa de tots els cossos implicats en el procés disminueix en 1 g, llavors l'energia és igual a 9×1013 J, que equival a 3000 tones de combustible estàndard.

Aquestes proporcions tenen una importància primordial en l'anàlisi de transformacions nuclears. En la majoria de processos macroscòpics, es pot descuidar el canvi de massa i només es pot parlar de la llei de conservació de l'energia.

Seguim les transformacions de l'energia en algun exemple concret. Considereu tota la cadena de conversions d'energia necessàries per produir qualsevol peça en un torn (Fig. 1). Sigui l'energia inicial 1, la quantitat de la qual prenem com a 100%, s'obté a causa de la combustió completa d'una certa quantitat de combustible fòssil. Per tant, per al nostre exemple, el 100% de l'energia inicial està continguda en els productes de la combustió del combustible, que es troben a una temperatura elevada (uns 2000 K).

Els productes de combustió a la caldera de la central elèctrica, quan es refreden, ceden la seva energia interna en forma de calor a l'aigua i al vapor d'aigua. Tanmateix, per raons tècniques i econòmiques, els productes de combustió no es poden refredar a temperatura ambient. S'expulsen a través del tub a l'atmosfera a una temperatura d'uns 400 K, portant amb ells part de l'energia original. Per tant, només el 95% de l'energia inicial es transferirà a l'energia interna del vapor d'aigua.

El vapor d'aigua resultant entrarà a la turbina de vapor, on la seva energia interna es converteix inicialment parcialment en energia cinètica de les cordes de vapor, que després es transmetrà com a energia mecànica al rotor de la turbina.

Només una part de l'energia del vapor es pot convertir en energia mecànica. La resta es dóna a l'aigua de refrigeració quan el vapor es condensa al condensador. En el nostre exemple, vam suposar que l'energia transferida al rotor de la turbina seria d'un 38%, que correspon aproximadament a l'estat de coses de les centrals elèctriques modernes.

En convertir l'energia mecànica en energia elèctrica a causa de l'anomenada Les pèrdues en joule als bobinats del rotor i de l'estator del generador perdran aproximadament un 2% de l'energia. Com a resultat, al voltant del 36% de l'energia inicial anirà a la xarxa.

Un motor elèctric convertirà només una part de l'energia elèctrica que se li subministra en energia mecànica per fer girar el torn. En el nostre exemple, al voltant del 9% de l'energia en forma de calor Joule als bobinats del motor i calor de fricció als seus coixinets s'alliberarà a l'atmosfera circumdant.

Així, només el 27% de l'energia inicial es lliurarà als òrgans de treball de la màquina. Però els contratemps energètics tampoc acaben aquí. Resulta que la major part de l'energia durant el mecanitzat d'una peça es gasta en fricció i en forma de calor s'elimina amb el líquid que refreda la peça. Teòricament, només una fracció molt petita (en el nostre exemple s'assumeix un 2%) de l'energia inicial seria suficient per obtenir la part desitjada de la part original.

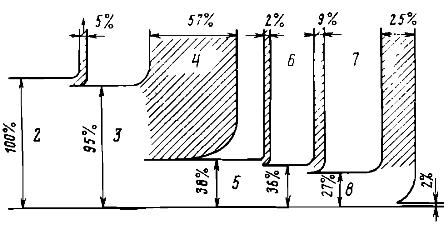
Arròs. 1. Diagrama de transformacions d'energia durant el processament d'una peça en un torn: 1 — pèrdua d'energia amb gasos d'escapament, 2 — energia interna dels productes de combustió, 3 — energia interna del fluid de treball — vapor d'aigua, 4 — calor alliberada pel refredament aigua en un condensador de turbina, 5 — energia mecànica del rotor d'un generador de turbina, 6 — pèrdues en el generador elèctric, 7 — residus en l'accionament elèctric de la màquina, 8 — energia mecànica de gir de la màquina, 9 — fricció el treball, que es converteix en calor, separat del líquid, la part de refrigeració, 10 - augmentant l'energia interna de la peça i els xips després del processament ...

De l'exemple considerat, es poden extreure almenys tres conclusions molt útils, si es considera bastant típic.

En primer lloc, a cada pas de la conversió d'energia es perd una part... Aquesta afirmació no s'ha d'entendre com una violació de la llei de conservació de l'energia. Es perd per l'efecte útil pel qual es realitza la transformació corresponent. La quantitat total d'energia després de la conversió es manté sense canvis.

Si el procés de conversió i transferència d'energia té lloc en una determinada màquina o aparell, aleshores l'eficiència d'aquest dispositiu es caracteritza normalment per l'eficiència (eficiència)... A la fig. 2.

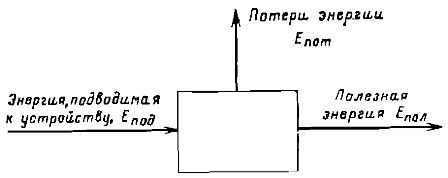
Arròs. 2. Esquema per determinar l'eficiència d'un dispositiu que converteix energia.

Utilitzant la notació que es mostra a la figura, l'eficiència es pot definir com a Eficiència = Epol/Epod

És evident que en aquest cas, basant-se en la llei de conservació de l'energia, hi ha d'haver Epod = Epol + Epot

Per tant, l'eficiència també es pot escriure de la següent manera: eficiència = 1 — (Epot / Epol)

Tornant a l'exemple mostrat a la FIG. 1, podem dir que l'eficiència de la caldera és del 95%, l'eficiència de convertir l'energia interna del vapor en treball mecànic és del 40%, l'eficiència del generador elèctric és del 95%, l'eficiència és: l'accionament elèctric d'un màquina: 75%, i l'eficiència del processament real de la peça és d'aproximadament un 7%.

En el passat, quan encara no es coneixien les lleis de la transformació de l'energia, el somni de la gent era crear l'anomenada màquina de moviment perpetu, un dispositiu que fes un treball útil sense gastar energia. Aquest motor hipotètic, l'existència del qual violaria la llei de conservació de l'energia, avui s'anomena màquina de moviment perpetu del primer tipus, en oposició a una màquina de moviment perpetu del segon tipus. Avui, per descomptat, ningú pren seriosament la possibilitat de crear una màquina de moviment perpetu del primer tipus.

En segon lloc, totes les pèrdues d'energia es converteixen finalment en calor, que s'allibera a l'aire atmosfèric o a l'aigua dels embassaments naturals.

En tercer lloc, les persones acaben utilitzant només una petita fracció de l'energia primària que es gasta per obtenir l'efecte beneficiós rellevant.

Això és especialment evident quan es miren els costos de transport d'energia. En la mecànica idealitzada, que no considera les forces de fricció, les càrregues en moviment en el pla horitzontal no requereixen energia.

En condicions reals, tota l'energia que consumeix un vehicle s'utilitza per superar les forces de fricció i les forces de resistència de l'aire, és a dir, en definitiva, tota l'energia consumida en el transport es converteix en calor. En aquest sentit, són interessants les xifres següents, que caracteritzen el treball de moure 1 tona de càrrega a una distància d'1 km amb diferents tipus de transport: avió — 7,6 kWh / (t-km), cotxe — 0,51 kWh / ( t- km) , tren-0,12 kWh / (t-km).

Així, el mateix efecte beneficiós es pot aconseguir amb el transport aeri a costa d'un consum d'energia 60 vegades més gran que amb el ferrocarril. Per descomptat, un alt consum d'energia proporciona un estalvi de temps important, però fins i tot a la mateixa velocitat (cotxe i tren), els costos energètics difereixen 4 vegades.

Aquest exemple suggereix que les persones sovint fan compromisos amb l'eficiència energètica per assolir altres objectius, com ara la comoditat, la velocitat, etc. Per regla general, l'eficiència energètica del procés ens interessa poc: la tècnica general i la les avaluacions econòmiques de l'eficiència dels processos són importants... Però a mesura que augmenta el preu dels components d'energia primària, el component energètic en les avaluacions tècniques i econòmiques adquireix cada cop més importància.