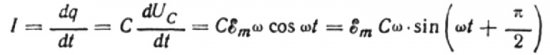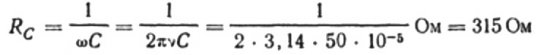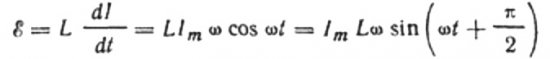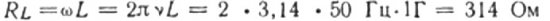Resistència capacitiva i inductiva en un circuit de corrent altern

Si incloem un condensador en un circuit de corrent continu, trobem que té una resistència infinita perquè un corrent continu simplement no pot passar pel dielèctric entre les plaques, ja que un dielèctric per definició no condueix un corrent elèctric continu.

Un condensador trenca el circuit de corrent continu. Però si ara s'inclou el mateix condensador al circuit de corrent altern, resulta que el seu condensador no sembla trencar-se completament, simplement alterna i es carrega, és a dir, la càrrega elèctrica es mou i el corrent al circuit extern és mantingut.

Basant-nos en la teoria de Maxwell en aquest cas, podem dir que el corrent de conducció altern dins del condensador encara està tancat, només en aquest cas, pel corrent de polarització. Això vol dir que el condensador del circuit de CA actua com un tipus de resistència de valor finit. Aquesta resistència s'anomena capacitiva.

La pràctica ha demostrat durant molt de temps que la quantitat de corrent altern que flueix per un conductor depèn de la forma d'aquest conductor i de les propietats magnètiques del medi que l'envolta.Amb un cable recte, el corrent serà el més gran, i si el mateix cable s'enrotlla en una bobina amb un gran nombre de voltes, el corrent serà menor.

I si s'introdueix un nucli ferromagnètic a la mateixa bobina, el corrent disminuirà encara més. Per tant, el cable proporciona corrent altern no només amb una resistència ohmica (activa), sinó també amb una resistència addicional, depenent de la inductància del cable. Aquesta resistència s'anomena. inductiu.

El seu significat físic és que un corrent canviant en un conductor d'una certa inductància inicia un EMF d'autoinducció en aquest conductor, que tendeix a evitar canvis en el corrent, és a dir, tendeix a reduir el corrent. Això equival a augmentar la resistència del cable.

Capacitat en el circuit de CA

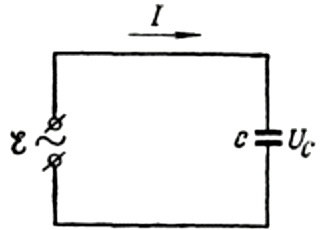
Primer, parlem de la resistència capacitiva amb més detall. Suposem que un condensador de capacitat C està connectat a una font de corrent altern sinusoïdal, aleshores la FEM d'aquesta font es descriu amb la fórmula següent:

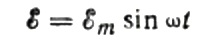
Ignorarem la caiguda de tensió als cables de connexió, ja que sol ser molt petita i es pot considerar per separat si cal. Suposem ara que la tensió a través de les plaques del condensador és igual a la tensió de la font de CA. Llavors:

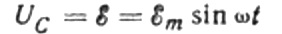
En un moment donat, la càrrega d'un condensador depèn de la seva capacitat i de la tensió entre les seves plaques. Aleshores, donada la font coneguda que es va esmentar anteriorment, obtenim una expressió per trobar la càrrega a les plaques del condensador per la tensió de la font:

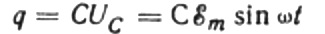
Sigui durant un temps infinitesimal dt la càrrega del condensador canvia en dq, aleshores un corrent I fluirà pels cables des de la font fins al condensador igual a:

El valor de l'amplitud actual serà igual a:

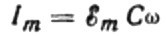
Aleshores, l'expressió final del corrent serà:

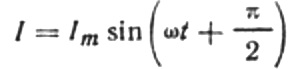
Reescriurem la fórmula de l'amplitud actual de la següent manera:

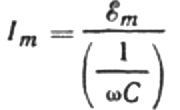
Aquesta relació és la llei d'Ohm, on el recíproc del producte de la freqüència angular i la capacitat juga el paper de la resistència, i en realitat és una expressió per trobar la capacitat d'un condensador en un circuit de corrent altern sinusoïdal:

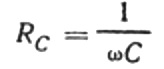
Això vol dir que la resistència capacitiva és inversament proporcional a la freqüència angular del corrent i la capacitat del condensador. És fàcil entendre el significat físic d'aquesta dependència.

Com més gran sigui la capacitat del condensador al circuit de CA i més sovint canvia la direcció del corrent en aquest circuit, en última instància, més càrrega total passa per unitat de temps a través de la secció transversal dels cables que connecten el condensador a la font de CA. Això vol dir que el corrent és proporcional al producte de la capacitat i la freqüència angular.

Per exemple, calculem la capacitat d'un condensador amb una capacitat elèctrica de 10 microfarads per a un circuit de corrent altern sinusoïdal amb una freqüència de 50 Hz:

Si la freqüència fos de 5000 Hz, el mateix condensador presentaria una resistència d'uns 3 ohms.

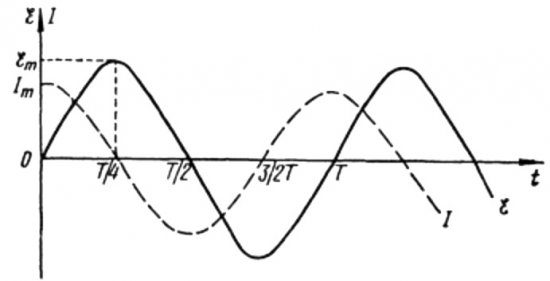
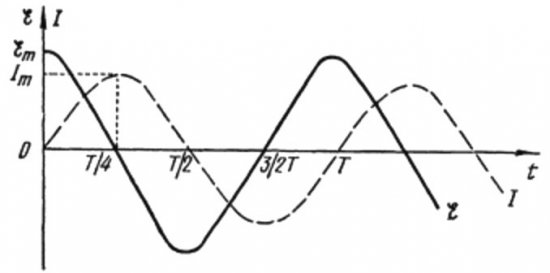
De les fórmules anteriors queda clar que el corrent i la tensió en un circuit de CA amb un condensador sempre canvien en diferents fases. La fase actual lidera la fase de tensió per pi / 2 (90 graus). Això vol dir que la intensitat màxima en el temps sempre existeix un quart de període abans que la tensió màxima. Així, a través de la resistència capacitiva, el corrent condueix la tensió en una quarta part del període de temps, o en 90 graus en fase.

Expliquem el significat físic d'aquest fenomen.En el primer instant de temps, el condensador es descarrega completament, de manera que la mínima tensió aplicada ja mou les càrregues de les plaques del condensador, creant un corrent.

A mesura que el condensador es carrega, la tensió a través de les seves plaques augmenta, això impedeix més flux de càrrega, de manera que el corrent al circuit disminueix malgrat els augments addicionals de la tensió aplicada a les plaques.

Això vol dir que si en el moment inicial de temps el corrent era màxim, aleshores quan la tensió assoleixi el seu màxim després d'un quart de període, el corrent s'aturarà completament.

Al començament del període, el corrent és màxim i el voltatge és mínim i comença a augmentar, però després d'un quart del període, el voltatge arriba al màxim, però el corrent ja ha baixat a zero en aquest moment. Així, resulta que la tensió porta la tensió una quarta part del període.

Resistència inductiva de CA

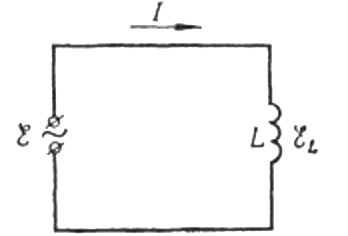
Ara tornem a la resistència inductiva. Suposem que un corrent sinusoïdal altern flueix per una bobina d'inductància. Es pot expressar com:

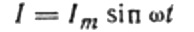
El corrent és degut a la tensió alterna aplicada a la bobina. Això significa que apareixerà un EMF d'autoinducció a la bobina, que s'expressa de la següent manera:

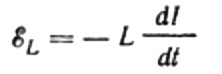
De nou, descuidem la caiguda de tensió als cables que connecten la font EMF a la bobina. La seva resistència òhmica és molt baixa.

Deixeu que la tensió alterna aplicada a la bobina en qualsevol instant de temps estigui completament equilibrada per l'EMF d'autoinducció que s'origina d'igual en magnitud, però de direcció oposada:

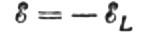
Aleshores tenim dret a escriure:

Com que l'amplitud de la tensió aplicada a la bobina és:

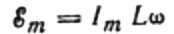
obtenim:

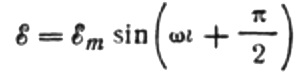
Expressem el corrent màxim de la manera següent:

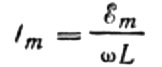
Aquesta expressió és essencialment la llei d'Ohm. Una quantitat igual al producte de la inductància i la freqüència angular juga aquí el paper de resistència i no és més que la resistència inductiva de l'inductor:

Per tant, la resistència inductiva és proporcional a la inductància de la bobina i la freqüència angular del corrent altern a través d'aquesta bobina.

Això es deu al fet que la resistència inductiva es deu a la influència de l'EMF d'auto-inducció sobre la tensió de la font, - EMF d'auto-inducció tendeix a reduir el corrent i, per tant, aporta resistència al circuit. La magnitud de la fem d'autoinducció, com se sap, és proporcional a la inductància de la bobina i la velocitat de canvi del corrent que la travessa.

Per exemple, calculem la resistència inductiva d'una bobina amb una inductància d'1 H, que s'inclou en un circuit amb una freqüència de corrent de 50 Hz:

Si la freqüència de la bola fos de 5000 Hz, aleshores la resistència de la mateixa bobina seria d'aproximadament 31.400 ohms Recordeu que la resistència ohmica del cable de la bobina sol ser d'uns pocs ohms.

A partir de les fórmules anteriors, és obvi que els canvis en el corrent a través de la bobina i la tensió en ella es produeixen en diferents fases, i la fase del corrent és sempre menor que la fase de la tensió a pi / 2. Per tant, el El corrent màxim es produeix un quart de període després de l'inici de l'estrès màxim.

En la resistència inductiva, el corrent retarda la tensió en 90 graus a causa de l'efecte de frenada de l'EMF autoinduït, que impedeix que el corrent canviï (tant augmenta com disminueix), de manera que el corrent màxim s'observa al circuit amb la bobina més tard. que la tensió màxima.

Acció combinada de bobina i condensador

Si connecteu una bobina amb un condensador en sèrie amb un circuit de corrent altern, la tensió de la bobina avançarà la tensió del condensador en el temps mig període, és a dir, 180 graus en fase.

S'anomenen resistències capacitiva i inductiva reactius… L'energia no es gasta en resistència reactiva com en resistència activa. L'energia emmagatzemada al condensador es retorna periòdicament a la font quan desapareix el camp elèctric del condensador.

Passa el mateix amb una bobina: com que el camp magnètic de la bobina és creat pel corrent, l'energia que hi ha s'acumula durant un quart del període, i durant el següent quart del període torna a la font. En aquest article, hem parlat del corrent altern sinusoïdal, per al qual aquestes normes es segueixen estrictament.

En els circuits sinusoïdals de CA, s'anomenen inductors amb nucli sufocants'utilitzen tradicionalment per limitar el corrent. El seu avantatge respecte als reòstats és que l'energia no es dissipa en grans quantitats com a calor.