Circuits elèctrics amb corrent no sinusoïdal

Corrents no sinusoïdals i la seva descomposició

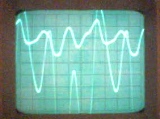En un circuit elèctric, els corrents no sinusoïdals es poden produir per dos motius:

1. el circuit elèctric en si és lineal, però una tensió no sinusoïdal actua sobre el circuit,

2. la tensió que actua sobre el circuit és sinusoïdal, però el circuit elèctric conté elements no lineals.

Hi podria haver ambdues raons. Aquest capítol tracta dels circuits només per al primer punt. En aquest cas, les tensions no sinusoïdals es consideren periòdiques.

Els generadors de polsos periòdics s'utilitzen en diversos dispositius d'enginyeria de ràdio, automatització, telemecànica. La forma dels polsos pot ser diferent: serra, esglaonada, rectangular (Fig. 1).

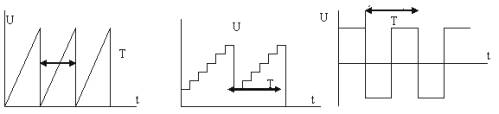
Figura 1. Formes de pols

Els fenòmens que ocorren en un circuit elèctric lineal sota tensions periòdiques però no sinusoïdals són més fàcils d'estudiar si la corba de tensió s'expandeix en una sèrie de Fourier trigonomètrica:

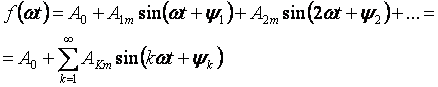
El primer terme de la sèrie A0 s'anomena component constant o harmònic zero, el segon terme de la sèrie

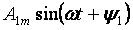
— l'harmònic fonamental o primer i tots els altres membres de la forma

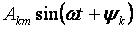
perquè k> 1 s'anomenen harmònics superiors.

Si a l'expressió (3.1) obrim el sinus de la suma, podem passar a una altra forma d'escriure la sèrie:

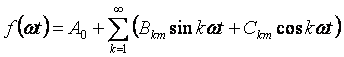Si la funció és simètrica respecte a l'eix de les abscisses, aleshores la sèrie no conté cap component constant. Si la funció és simètrica respecte a l'eix d'ordenades, aleshores la sèrie no conté sinus. La funció és simètrica respecte a l'origen i no conté cosinus.

Alguns exemples d'expansió de sèries es donen en una taula. 1 i també estan disponibles a la literatura de referència.

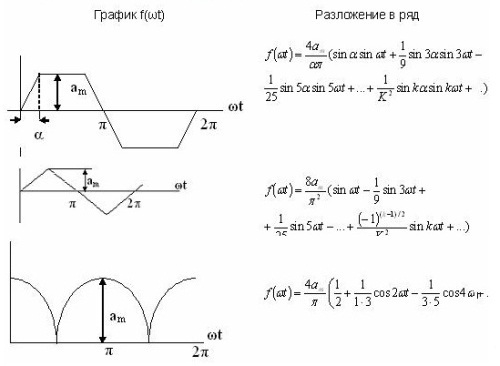
Taula 1. Expansió de la sèrie de Fourier

Càlcul de circuits de corrent no sinusoïdal

El circuit es calcula per a cada harmònic segons el model. El circuit es calcula tantes vegades com harmònics hi hagi en la tensió que actua sobre el circuit. En aquest cas, cal tenir en compte una sèrie de característiques.

Cal tenir en compte que la resistència de l'element inductiu augmenta a mesura que augmenta el nombre harmònic

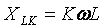
i l'element capacitiu, per contra, disminueix:

També s'ha de tenir en compte que la component constant del corrent no passa pel condensador i la inductància no és una resistència.

A més, no s'ha d'oblidar els possibles fenòmens de ressonància no només a l'harmònic fonamental, sinó també als harmònics superiors.

Esquemes vectorials es pot representar per a cada harmònic per separat.

Segons el principi de superposició, el corrent de cada branca pot consistir en la suma de termes individuals (harmònics zero, fonamentals i superiors):

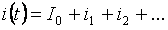
El valor rms del corrent de branca total es pot determinar pel valor mitjà dels corrents harmònics individuals:

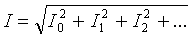
La potència activa del corrent no sinusoïdal és igual a la suma de les potències actives dels harmònics individuals:

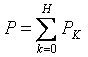
A continuació es mostra un exemple general per calcular circuits de corrent no sinusoïdals. Tots els corrents, voltatges, resistències tindran dos índexs: el primer dígit significa el número de branca i el segon dígit el nombre harmònic. Voltatge d'entrada:

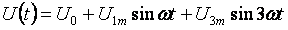
• Component permanent

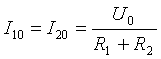
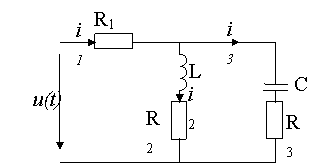
Figura 2. Esquema elèctric

• Harmònic major:

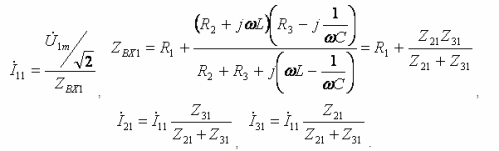
• Tercer harmònic:

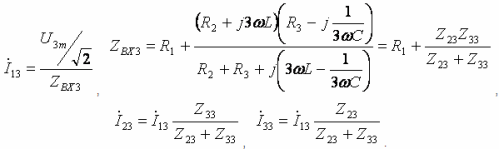
Llegeix també: Els esquemes de rectificació de CA a CC més comuns