Principi i mètodes de determinació indirecta del factor de potència en el circuit de corrent altern

Factor de potència o cosinus phi, respecte a l'usuari de corrent altern sinusoïdal, és la relació entre el consum d'energia activa P i la potència total S que es subministra a aquest usuari des de la xarxa.

Potència total S, en el cas general, es pot definir com el producte dels valors efectius (arrel quadrada mitjana) del corrent I i la tensió U en el circuit considerat, i la potència activa P, que consumeix de manera irreversible per l'usuari per al funcionament de l'obra.

Potència reactiva Q, tot i que forma part de la potència total, però, no es consumeix per realitzar treballs, sinó que només participa en la creació de camps elèctrics i magnètics alterns en alguns elements del circuit de l'usuari.

excepte mesura directa del factor de potència Ús de dispositius electrodinàmics - mesuradors de fase, hi ha mètodes indirectes força lògics que permeten comprendre matemàticament amb precisió el valor d'aquesta magnitud elèctrica tan important que caracteritza l'usuari en un circuit de corrent altern sinusoïdal.

Vegem les dades mètodes indirectes en detalls, Entenem el principi de mesura indirecta del factor de potència.

Mètode voltímetre, amperímetre i wattmetre

Wattmetre electrodinàmic amb una resistència activa addicional al circuit de la seva bobina mòbil indica el valor de potència extremadament activa consumida al circuit de CA P.

Si ara, utilitzant un voltímetre i un amperímetre, mesurem els valors mitjans del corrent I i de la tensió U que actuen en el circuit de la càrrega en estudi, aleshores, multiplicant aquests dos paràmetres, obtindrem només la potència total S .

Aleshores, el factor de potència (cosinus phi) d'una càrrega donada es pot trobar fàcilment mitjançant la fórmula:

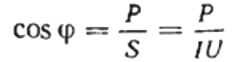
Aquí, si voleu, també podeu trobar el valor de la potència reactiva Q, la resistència total del circuit z Llei d'Ohm, així com la resistència activa i reactiva, simplement construint o representant un triangle de resistència, i després utilitzant el teorema de Pitàgores:

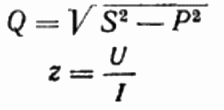
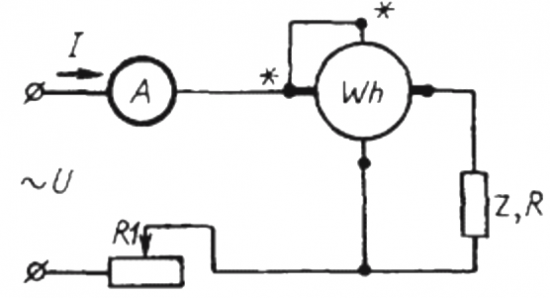
Mètode comptador i amperímetre

Per utilitzar aquest mètode, cal muntar un circuit en què el més senzill estigui connectat en sèrie amb la càrrega Z i l'amperímetre. comptador d'electricitat Wh.

Durant un període de temps t, de l'ordre d'un minut, caldrà calcular el nombre de revolucions del disc N, que mostrarà la quantitat d'energia activa gastada durant un temps determinat (és a dir, tenint en compte la factor de potència).

Aquí: el nombre de revolucions del disc N, el coeficient k és la quantitat d'energia per revolució, I i U són el corrent i la tensió rms respectivament, t és el temps per comptar les revolucions, el cosinus phi és el factor de potència:

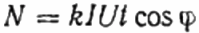
Aleshores, en comptes de l'usuari Z estudiat, la càrrega activa R s'inclou al circuit mitjançant el mateix comptador, però no directament, sinó a través del reòstat R1 (aconseguint el mateix corrent I que en el primer cas, amb l'usuari Z). El nombre de revolucions del disc N1 es manté durant el mateix temps t. Però aquí, com que la càrrega està activa, el cosinus phi (factor de potència) és certament igual a 1. Per tant:

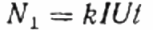
Aleshores, la relació de revolucions del comptador de disc s'enregistra durant el mateix període de temps en el primer i el segon cas. Aquest serà el cosinus phi, és a dir, el factor de potència de la primera càrrega (relatiu a una càrrega purament activa amb el mateix actual):

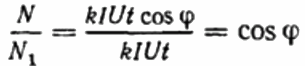
Mètode de tres amperímetres

Per determinar el factor de potència en un circuit de corrent sinusoïdal mitjançant tres amperímetres, primer heu de muntar el circuit següent:

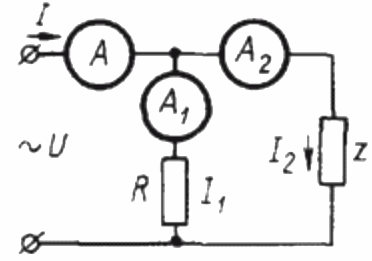
Aquí Z és una càrrega el factor de potència de la qual s'ha de determinar i R és una càrrega purament activa.

Com que la càrrega R és purament activa, el corrent I1 en qualsevol instant de temps està en fase amb la tensió alterna U aplicada a aquesta càrrega, en aquest cas, el corrent I és igual a la suma geomètrica dels corrents I1 i I2. Ara construirem a partir d'aquesta posició un diagrama vectorial dels corrents:

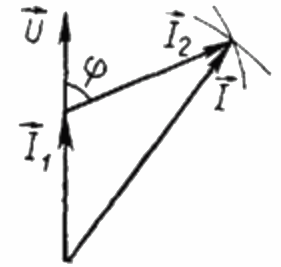
Al diagrama vectorial dels corrents, l'angle agut entre el corrent I1 i el corrent I2 és l'angle phi, el cosinus del qual (de fet, el valor del factor de potència) es pot trobar a partir d'una taula especial de valors. de funcions trigonomètriques o calculades per la fórmula:

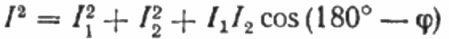
A partir d'aquí podem expressar cosinus phi, és a dir, el factor de potència desitjat:

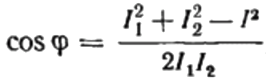
El signe del factor de potència trobat («+» o «-«) indicarà la naturalesa de la càrrega. Si el factor de potència (cosinus phi) és negatiu, la càrrega és de naturalesa capacitiva. Si el factor de potència és un valor positiu, aleshores la naturalesa de la càrrega és inductiva.