Alimentació de la xarxa trifàsica: activa, reactiva, plena

Els valors de la potència activa total i reactiva total del circuit trifàsic són iguals a les sumes de la potència activa i reactiva de cadascuna de les tres fases A, B i C, respectivament. Aquesta afirmació s'il·lustra a continuació. fórmules:

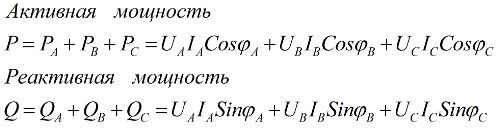
aquí Ua, Ub, Uc, Ia, Ib, Ic són els valors de les tensions i corrents de fase i φ és el desplaçament de fase.

Quan la càrrega és simètrica, és a dir, en condicions en què la potència activa i reactiva de cadascuna de les fases són iguals entre si, per trobar la potència total del circuit multifàsic, n'hi ha prou amb multiplicar el valor de la potència de fase per el nombre de fases implicades. La potència total es determina en funció dels valors obtinguts dels seus components actius i reactius:

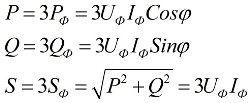
A les fórmules anteriors, els valors de fase de les quantitats es poden expressar en termes dels seus valors lineals, que diferiran per als esquemes de connexió estrella o triangle per als usuaris, però les fórmules de potència seran finalment les mateixes:

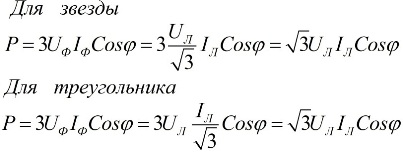
De les expressions anteriors es desprèn que, independentment de l'esquema de connexió dels receptors d'energia elèctrica, ja sigui un triangle o una estrella, si la càrrega és simètrica, les fórmules per trobar la potència tindran la mateixa forma, tant per a un triangle i per a una estrella:

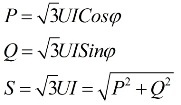
Aquestes fórmules mostren valors lineals de tensió i corrent i s'escriuen sense subíndex. Normalment es troba aquesta notació, sense subíndexs, és a dir, si no hi ha subíndexs, ens referim a valors lineals.

Un dispositiu de mesura especial, anomenat wattmetre... Les seves lectures estan determinades per la fórmula:

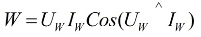
en la fórmula anterior, Uw i Iw són els vectors de la tensió aplicada a la càrrega i el corrent que hi circula.

La naturalesa de la càrrega activa i el diagrama de connexió de fases poden ser diferents, per tant, depenent de les circumstàncies específiques, els diagrames de connexió del vatímetre seran diferents.

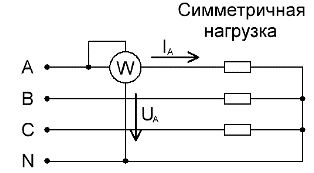
Per a circuits trifàsics carregats simètricament, per a una mesura aproximada de la potència activa total, si no es requereix una gran precisió, n'hi ha prou amb un vatímetre connectat a una sola de les fases. Després d'això, per obtenir el valor de la potència activa de tot el circuit, cal multiplicar les lectures del vatímetre pel nombre de fases:

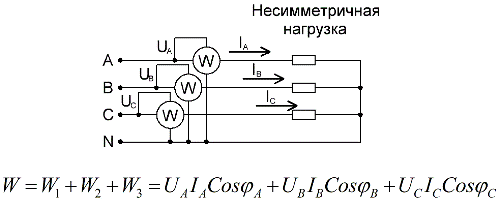
Per a un circuit de quatre fils amb un cable neutre, per mesurar amb precisió la potència activa, es necessiten tres wattmetres, cadascun dels quals es llegeix i després es suma per obtenir un valor per a la potència total del circuit:

Si no hi ha cable neutre en un circuit trifàsic, dos vatímetres són suficients per mesurar la potència total, fins i tot si la càrrega està desequilibrada.

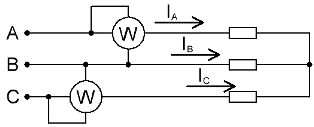
En absència d'un conductor neutre, els corrents de fase estan interconnectats segons la primera llei de Kirchhoff:

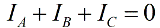
Aleshores, la suma de les lectures d'un parell de wattmetres serà igual a:

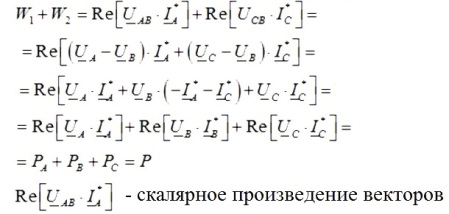
Per tant, si afegiu les lectures d'un parell de vatímetres, s'obté la potència activa total del circuit trifàsic que s'estudia, i les lectures dels vatímetres dependran tant de la mida de la càrrega com de la seva naturalesa.

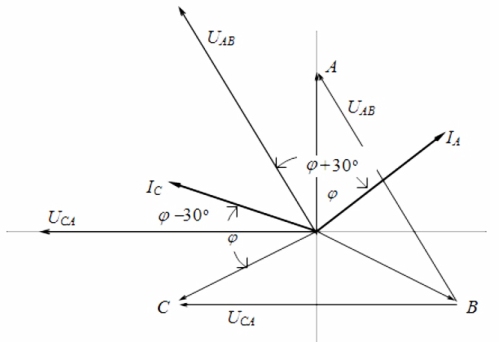
Si observem el diagrama vectorial de corrents i tensions en relació amb una càrrega simètrica, es pot concloure que les lectures dels vatímetres es determinen per les fórmules següents:

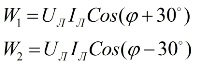
Després d'analitzar aquestes expressions, es pot entendre que amb una càrrega purament activa, quan φ = 0, les lectures dels dos wattmetres seran iguals entre si, és a dir, W1 = W2.

Amb la inductància de càrrega activa, quan 0 ≤ φ ≤ 90 °, les lectures del vatímetre 1 seran inferiors a les del vatímetre 2, és a dir, W1 60 °, les lectures del vatímetre 1 seran negatives, és a dir, W1 <0.

Amb una naturalesa activa-capacitiva de la càrrega, quan 0 ≥ φ≥ -90 °, les lectures del vatímetre 2 seran més petites que el vatímetre 1, és a dir, W1> W2. A φ <-60 °, les lectures del vatímetre 2 es tornaran negatives.