Corrent altern monofàsic
Adquisició de corrent altern
Si el fil A fa girar en el flux magnètic format pels dos pols de l'imant en el sentit de les agulles del rellotge (Fig. 1), aleshores quan el cable travessa les línies del camp magnètic, induirà e. d. s el valor de la qual ve determinat per l'expressió
E = Blvsinα,
on B és la inducció magnètica en T, l és la longitud del cable en m, v és la velocitat del cable en m / s, α - l'angle en què el cable creua les línies del camp magnètic.
Sigui B, I i v en aquest cas que es mantenen constants, aleshores l'induït e. etc. c) només dependrà de l'angle α en què el cable travessa el camp magnètic. Així, al punt 1, quan el cable es mou al llarg de les línies del camp magnètic, el valor de la fem induïda. etc. p serà zero quan el cable es mogui al punt 3 oe. etc. v. tindran la màxima importància, ja que les línies de força seran travessades pel conductor en la direcció perpendicular a elles, i finalment, p. etc. v. tornarà a arribar a zero si el cable es mou al punt 5.
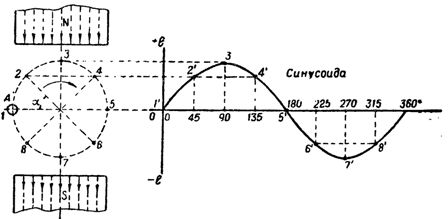
Arròs. 1. Canviar la e induïda. etc. pp en un fil que gira en un camp magnètic
En els punts intermedis 2 i 4, en què el cable travessa les línies de força amb un angle α = 45 °, el valor de la fem induïda. etc. c serà corresponentment menor que al punt 3. Així, quan el cable es gira del punt 1 al punt 5, és a dir, 180 °, l'e induïda. etc. v. canvia de zero a màxim i torna a zero.
És força obvi que en una nova rotació del cable A a través d'un angle de 180 ° (a través dels punts 6, 7, 8 i 1), la naturalesa del canvi en l'e induït. etc. p. serà el mateix, però la seva direcció canviarà al contrari, ja que el cable travessarà les línies del camp magnètic ja per sota de l'altre pol, la qual cosa equival a creuar-les en la primera direcció oposada.
Per tant, quan el cable es gira 360 °, l'e. etc. v. no només canvia de magnitud tot el temps, sinó que també canvia la seva direcció dues vegades.
Si el cable està tancat a una certa resistència, apareixerà el cable electricitat, variant també en mida i direcció.
El corrent elèctric, que canvia contínuament en magnitud i direcció, s'anomena corrent altern.
Què és una ona sinusoïdal?
La naturalesa del canvi e. etc. (actual) per a una volta del cable per a una major claredat, es representen gràficament mitjançant una corba. Atès que el valor d'e. etc. c) proporcional a sinα, doncs, havent fixat determinats angles, és possible, amb l'ajuda de taules, determinar el valor del sinus de cada angle, i a l'escala adequada construir una corba per al canvi de e. etc. c.Per fer-ho, a l'eix horitzontal deixarem de banda els angles de gir del fil, i a l'eix vertical, a l'escala adequada, l'e induït. etc. amb
Si s'indica prèviament a la fig.1 connecteu els punts amb una línia corba suau, aleshores donarà una idea de la magnitud i la naturalesa del canvi en l'e induïda. etc. (corrent) en qualsevol posició del conductor en un camp magnètic. A causa del fet que el valor de l'induït e. etc. p.en qualsevol moment ve determinat pel sinus de l'angle en què el cable travessa el camp magnètic mostrat a la fig. 1 corba s'anomena sinusoide, i e. etc. s. — sinusoïdal.
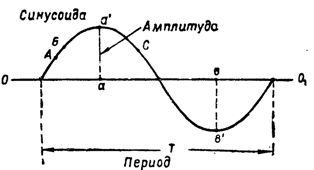
Arròs. 2. La sinusoide i els seus valors característics
Els canvis que hem observat e. etc. c) Sinusoïdalment corresponen a la rotació del cable en un camp magnètic en un angle de 360 °. Quan el cable es gira els següents 360 °, els canvis en l'e induït. etc. s.(i corrent) tornaran a aparèixer en ona sinusoïdal, és a dir, es repetiran periòdicament.
En conseqüència, provocat per aquest e. etc. c.s'anomena corrent elèctric corrent altern sinusoïdal... És força obvi que la tensió que podem mesurar per nosaltres als extrems del fil A, en presència d'un circuit extern tancat, també canviarà de manera sinusoïdal.
El corrent altern obtingut fent girar un cable en un flux magnètic o un sistema de cables connectats en una bobina s'anomena corrent altern monofàsic.
Els corrents alterns sinusoïdals són els més utilitzats en tecnologia. Tanmateix, podeu trobar corrents alterns que no canvien segons la llei sinusoïdal. Aquests corrents alterns s'anomenen no sinusoïdals.
Vegeu també: Què és el corrent altern i en què es diferencia del corrent continu
Amplitud, període, freqüència del corrent altern monofàsic
Força actual, canviant al llarg d'una sinusoide, canvia contínuament. Així, si al punt A (Fig. 2) el corrent és igual a 3a, aleshores al punt B ja serà més gran.En algun altre punt de la sinusoide, per exemple al punt C, el corrent tindrà ara un nou valor, i així successivament.
La intensitat del corrent en determinats moments quan canvia al llarg d'una sinusoide s'anomena valors de corrent instantani.
El valor instantani més gran d'un corrent altern monofàsic s'anomena quan canvia al llarg d'una amplitud sinusoïdal... És fàcil veure que per una volta de cable el corrent arriba al seu valor d'amplitud dues vegades. Un dels valors de aa 'és positiu i es dibuixa des de l'eix 001 i l'altre bv' és negatiu i es dibuixa cap avall des de l'eix.
El temps durant el qual la induïda e. etc. (o la força actual) passa per tot el cicle de canvis, l'anomenat cicle mensual T (Fig. 2). El període normalment es mesura en segons.
El recíproc del període s'anomena freqüència (f). En altres paraules, freqüència de corrent altern és el nombre de períodes per unitat de temps, és a dir. en segonsdoo. Així, per exemple, si un corrent altern en 1 segon assumeix els mateixos valors i direcció deu vegades, la freqüència d'aquest corrent altern serà de 10 períodes per segon.
Per mesurar la freqüència, en comptes del nombre de períodes per segon, s'utilitza una unitat anomenada hertz (hertz). Una freqüència d'1 hertz és igual a una freqüència d'1 lps/s. Quan es mesuren altes freqüències, és més convenient utilitzar una unitat 1000 vegades més gran que l'hertz, és a dir. kilohertz (kHz), o 1.000.000 de vegades més gran que hertz — megahertz (mhz).
Els corrents alterns utilitzats en tecnologia, segons la freqüència, es poden dividir en corrents de baixa freqüència i corrents d'alta freqüència.
Valor rms de CA
El corrent continu que passa pel cable l'escalfa. Si feu servir corrent altern a través del cable, el cable també s'escalfarà.Això és comprensible, perquè tot i que el corrent altern canvia de direcció tot el temps, l'alliberament de calor no depèn en absolut de la direcció del corrent al cable.
Quan el corrent altern passa per una bombeta, el seu filament brillarà. A una freqüència de corrent altern estàndard de 50 Hz, no hi haurà parpelleig de la llum, perquè el filament de la bombeta incandescent, amb inèrcia tèrmica, no té temps de refredar-se en aquells moments en què el corrent al circuit és zero. L'ús de corrent altern amb una freqüència inferior a 50 Hz per a la il·luminació ara no és desitjable a causa del fet que apareixen fluctuacions desagradables i fatigants oculars en la intensitat de la bombeta.
Continuant amb l'analogia del corrent continu, podem esperar que es creï un corrent altern que flueix per un cable al seu voltant camp magnètic. En realitat, nEl corrent altern no crea un camp magnètic, sinó perquè el camp magnètic que crea també serà variable en direcció i magnitud.
Un corrent altern canvia tot el temps tant en magnitud com en direccióNS. Naturalment, sorgeix la pregunta de com mesurar bé la variable T i quin és el seu valor quan es canvia al llarg d'una sinusoide com a causant d'aquesta o aquella acció.
C Amb aquesta finalitat, es compara el corrent altern en funció de l'acció que produeix amb el corrent continu, el valor del qual es manté inalterable durant l'experiment.
Suposem que un corrent continu flueix per un cable de resistència constant de 10 A i es troba que el cable s'escalfa a una temperatura de 50 °.Si ara passem pel mateix cable no un corrent continu, sinó un corrent altern, i així escollim el seu valor (actuant, per exemple, amb un reòstat) de manera que el cable també s'escalfi a una temperatura de 50 °, aleshores en en aquest cas podem dir que l'acció del corrent altern és igual a l'acció del corrent continu.
Escalfar el cable en ambdós casos a la mateixa temperatura mostra que en una unitat de temps el corrent altern desprèn al cable la mateixa quantitat de calor que el corrent continu.
Un corrent sinusoïdal altern que emet per a una resistència determinada per unitat de temps la mateixa quantitat de calor que un corrent continu equivalent en magnitud a un corrent continu... Aquest valor de corrent s'anomena valor efectiu (Id) o efectiu del corrent altern. Per tant, per al nostre exemple, el valor efectiu del corrent altern serà de 10 A... En aquest cas, els valors màxims (pics) de corrent superaran els valors mitjans en magnitud.
L'experiència i els càlculs mostren que els valors efectius del corrent altern són més petits que els seus valors d'amplitud en √2 (1,41) vegades. Per tant, si es coneix el valor màxim del corrent, llavors el valor efectiu del corrent Id es pot determinar dividint l'amplitud del corrent Ia per √2, és a dir, Id = Aza/√2
Per contra, si es coneix el valor rms del corrent, es pot calcular el valor màxim del corrent, és a dir, Ia = Azd√2
Les mateixes relacions es mantindran per a l'amplitud i els valors rms d'e. etc. v. i tensions: Unitat = Ea /√2, Ud = Uа/√2
Els dispositius de mesura sovint mostren els valors reals, per tant, quan es fa notació, l'índex «d» sol ometre's, però no us heu d'oblidar d'això.
Impedància en circuits de CA
Quan els consumidors d'inductància i capacitat estan connectats al circuit de CA, s'han de tenir en compte tant l'actiu com la reactància (la reactància es produeix quan un condensador està encès o asfixia en un circuit de CA). Per tant, quan es determina el corrent que passa per aquest consumidor, cal dividir la tensió d'alimentació per la impedància del circuit (consumidor).
La impedància (Z) d'un circuit de corrent alterna monofàsic es determina per la fórmula següent:
Z = √(R2 + (ωL — 1 / ωC)2
on R és la resistència activa del circuit en ohms, L és la inductància del circuit en henries, C és la capacitat del circuit (condensador) en farads, ω - freqüència angular del corrent altern.
En circuits de corrent altern s'utilitzen diferents consumidors on cal tenir en compte els tres valors de R, L, C o només alguns d'ells. Al mateix temps, cal tenir en compte la freqüència angular del corrent altern.
Per a alguns usuaris, només es poden tenir en compte els valors de R i L als valors de freqüència de cantonada corresponents. Per exemple, a una freqüència de CA de 50 Hz bobina de solenoide o el bobinatge del generador només es pot considerar que conté resistència activa i inductiva. En altres paraules, la capacitat en aquest cas es pot descuidar. Aleshores, la impedància de CA d'aquest usuari es pot calcular mitjançant la fórmula:
Z = √(R2 + ω2L2)
Si una bobina d'aquest tipus o una bobina dissenyada per al funcionament de corrent altern està connectada a un corrent continu de la mateixa tensió, un corrent molt gran fluirà a través de la bobina, que pot provocar una generació de calor significativa i l'aïllament de la bobina es pot danyar. Al contrari, una petita corrent circularà per una bobina dissenyada per funcionar en un circuit de corrent continu i connectada a un circuit de corrent altern de la mateixa tensió, i l'aparell en què s'utilitza aquesta bobina no realitzarà l'acció requerida.
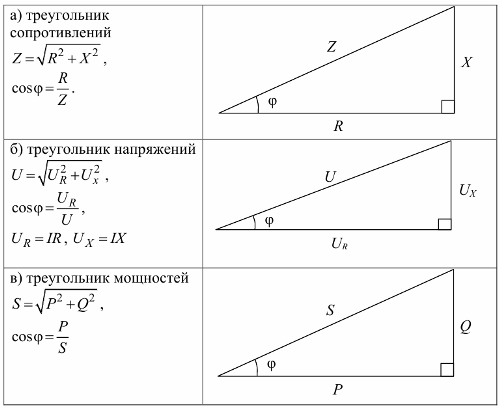
Triangle de resistència, triangle de tensió i triangle de potència:
