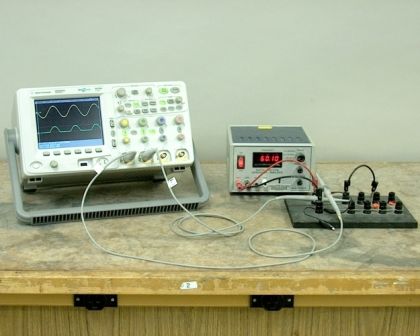
Corrent d'impuls

En diversos dispositius electrònics, per exemple, en equips electrònics i semiconductors, és a dir, en amplificadors, rectificadors, ràdios, generadors, televisors, així com en micròfons de carboni, telègrafs i molts altres dispositius, s'utilitzen àmpliament corrents i tensions ondulatòries... per no repetir el raonament dues vegades, només parlarem de corrents, però tot el que està relacionat amb les corrents també és cert per a les tensions.

Els corrents polsants que tenen una direcció constant però que canvien el seu valor poden ser diferents. De vegades, el valor actual canvia del valor diferent de zero més alt al més baix. En altres casos, el corrent es redueix a zero. Si circuit de corrent continu s'interromp a una freqüència determinada, i durant alguns intervals de temps no hi ha corrent al circuit.

A la fig. La figura 1 mostra gràfics de diferents corrents d'ona. A la fig. 1, a, b, el canvi de corrents es produeix segons corba sinusoïdal, però aquests corrents no s'han de considerar corrents alterns sinusoïdals, ja que el sentit (signe) del corrent no canvia. A la fig.1, c mostra un corrent format per polsos separats, és a dir, "xocs" de corrent de curta durada, separats entre si per pauses de major o menor durada, i sovint s'anomena corrent polsat. Els diferents corrents polsats es diferencien entre si en la forma i la durada dels polsos, així com en la velocitat de repetició.

És convenient considerar un corrent polsant de qualsevol tipus com la suma de dos corrents: directe i altern, anomenats corrents de termes o components. Qualsevol corrent pulsatori té components DC i AC. Això sembla estrany per a molts. De fet, al cap i a la fi, un corrent polsador és un corrent que flueix tot el temps en una direcció i canvia el seu valor.

Com es pot dir que conté corrent altern que canvia de direcció? No obstant això, si dos corrents —directes i alternes— passen simultàniament pel mateix cable, resulta que un corrent pulsatori circularà per aquest cable (Fig. 2). En aquest cas, l'amplitud del corrent altern no ha de superar el valor del corrent continu. Els corrents continus i alterns no poden circular per separat pel cable. S'afegeixen a un flux general d'electrons que té totes les propietats d'un corrent pulsante.

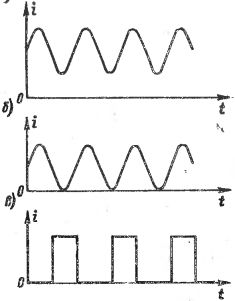
Arròs. 1. Gràfiques de diferents corrents d'ona

L'addició de corrents AC i DC es pot mostrar gràficament. A la fig. La figura 2 mostra els gràfics d'un corrent continu igual a 15 mA i un corrent altern amb una amplitud de 10 mA. Si sumem els valors d'aquests corrents per a punts individuals en el temps, tenint en compte les direccions (signes) dels corrents, obtenim el gràfic de corrent d'ona que es mostra a la fig. 2 amb una línia en negreta. Aquest corrent varia des d'un mínim de 5 mA fins a un màxim de 25 mA.

L'addició considerada de corrents confirma la validesa de la representació del corrent pulsatori com a suma de corrents continus i alterns. La correcció d'aquesta representació també es confirma pel fet que amb l'ajuda d'alguns dispositius és possible separar els components d'aquest corrent entre si.

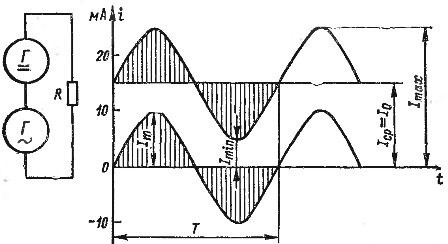
Arròs. 2. Obtenció d'un corrent pulsatori afegint corrent continu i altern.

Cal subratllar que qualsevol corrent sempre es pot representar com una suma de diversos corrents. Per exemple, un corrent de 5 A es pot considerar la suma de corrents 2 i 3 A que circulen en una direcció, o la suma de corrents 8 i 3 A que circulen en diferents direccions, és a dir, la diferència entre corrents 8 i 3 A. No és difícil trobar altres combinacions de dos o més corrents donant un total de 5 A.

Aquí hi ha una similitud total amb el principi d'addició i descomposició de forces. Si dues forces igualment dirigides actuen sobre qualsevol objecte, es poden substituir per una força comuna. Les forces que actuen en direccions oposades es poden substituir per una diferència unitaria. Per contra, una força donada sempre es pot considerar la suma de les forces igualment dirigides corresponents o la diferència entre les forces de direcció oposada.

No és necessari descompondre els corrents alterns directes o sinusoïdals en corrents components. Si substituïm el corrent polsant per la suma de corrents continus i alterns, aplicant les lleis conegudes dels corrents continus i alterns a aquests corrents components, és possible resoldre molts problemes i fer els càlculs necessaris relacionats amb el corrent polsador.

El concepte de corrent polsant com a suma de corrents continus i alterns és convencional.Per descomptat, no es pot suposar que en determinats intervals de temps els corrents directes i alterns flueixen realment entre si al llarg del cable. De fet, no hi ha dos fluxos d'electrons oposats.

En realitat, un corrent polsador és un únic corrent que canvia el seu valor amb el temps. És més correcte dir que la tensió pulsatòria o EMF pulsatòria es pot representar com la suma de les components constants i variables.

Per exemple, a la FIG. La figura 2 mostra com s'afegeix algebraicament la fem constant d'un generador a la fem variable d'un altre generador. Com a resultat, tenim un EMF pulsatori que provoca el corresponent corrent pulsatori. Condicionalment, però, es pot considerar que un EMF constant crea un corrent continu al circuit i un EMF altern, un corrent altern, que, quan es suma, forma un corrent pulsatori.

Cada corrent de pols es pot caracteritzar pels valors màxim i mínim d'Itax i Itin, així com els seus components constants i variables. La component constant es denota amb I0. Si el component altern és un corrent sinusoïdal, llavors la seva amplitud es denota amb It (totes aquestes magnituds es mostren a la figura 2).

No s'ha de confondre amb It i Itax. A més, el valor màxim de l'ona actual Imax no s'ha d'anomenar amplitud. El terme amplitud sol referir-se només als corrents alterns. Pel que fa al corrent pulsatori, només podem parlar de l'amplitud de la seva component variable.

La component constant del corrent polsador es pot anomenar el seu valor mitjà Iav, és a dir, el valor mitjà aritmètic. De fet, si tenim en compte els canvis en un període del corrent pulsatori que es mostra a la Fig.2, es veu clarament el següent: al primer mig cicle, s'afegeixen una sèrie de valors al corrent de 15 mA variant el component actual, que varia de 0 a 10 mA i torna a 0, i a la segona meitat -cicle, es resten exactament els mateixos valors actuals dels 15 mA actuals.

Per tant, el corrent de 15 mA és realment el valor mitjà. Com que el corrent és la transferència de càrregues elèctriques a través de la secció transversal del cable, aleshores Iav és el valor d'un corrent continu que en un període (o durant un nombre sencer de períodes) transporta la mateixa quantitat d'electricitat que aquest corrent polsador. .

Per al corrent altern sinusoïdal, el valor de Iav per període és zero perquè la quantitat d'electricitat que passa per la secció transversal del conductor en un mig període és igual a la quantitat d'electricitat que passa en sentit contrari durant un altre mig període. En els gràfics de corrents que mostren la dependència del corrent i en el temps t, la quantitat d'electricitat transportada pel corrent s'expressa per l'àrea de la figura limitada per la corba de corrent, ja que la quantitat d'electricitat ve determinada per la producte que ell.

Per a un corrent sinusoïdal, les àrees de les mitjaones positives i negatives són iguals.En el corrent pulsatori que es mostra a la fig. 2, durant el primer semestre, la quantitat d'electricitat transportada pel component de CA s'afegeix a la quantitat d'electricitat transportada per l'Iav actual (àrea ombrejada a la figura). I durant la segona meitat del cicle, es retira exactament la mateixa quantitat d'electricitat. Com a resultat, durant tot el període es transfereix la mateixa quantitat d'electricitat que amb un sol corrent continu Iav, és a dir, l'àrea del rectangle Iav T és igual a l'àrea limitada per la corba de corrent d'ona.

Així, la component constant o el valor mitjà del corrent està determinat per la transferència de càrregues elèctriques a través de la secció transversal del cable.

L'equació actual que es mostra a la Fig. 2 òbviament s'ha d'escriure de la forma següent:

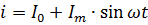
La potència del corrent de pols s'ha de calcular com la suma de les potències dels seus components. Per exemple, si el corrent que es mostra a la Fig. 2, passa per una resistència de resistència R, llavors la seva potència és

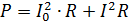
on I = 0,7Im és el valor rms de la component variable.

Podeu introduir el concepte del valor rms del corrent d'ona Id. La potència es calcula de la manera habitual:

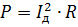
Igualant aquesta expressió a l'anterior i reduint-la amb R, obtenim:

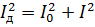
Les mateixes relacions es poden obtenir per a tensions.