Forces electrodinàmiques en parts actives d'estructures i dispositius
Les parts d'equips elèctrics i aparells de distribució sota tensió, quan hi passa corrent, estan exposades a forces electrodinàmiques... Com sabeu, aquestes forces actuen sobre qualsevol conductor portador de corrent situat a camp magnètic.
Les magnituds d'aquestes forces per a elements de commutació i dispositius de configuració simple es poden determinar a partir de la llei de Biot-Savard:
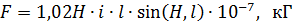
on (H, l) és l'angle format per la direcció del corrent i la direcció del camp magnètic; amb cables paral·lels és de 90 °.
Si dos conductors paral·lels es mouen en un corrent i un conductor amb un corrent i1 es troba en un camp magnètic amb un corrent i2 d'intensitat H = 0,2 • i2 / a, llavors la magnitud de la força que actua entre ells serà igual a
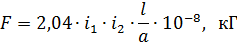
on i1 i i2 són els corrents del primer i segon cables, i; a és la distància entre els eixos dels cables, cm; l — longitud del cable, vegeu
La força que actua entre els cables els atrau els uns als altres amb la mateixa direcció de corrent en ells i els repel·leix en diferents direccions.
El valor més gran d'aquestes forces electrodinàmiques ve determinat pel màxim corrent de curtcircuit possible, és a dir, corrent de curtcircuit iy. Per tant, el moment inicial del curtcircuit (t = 0,01 s) és el més perillós pel que fa a la magnitud de les forces dinàmiques.
Quan un corrent de curtcircuit passa pel disjuntor o quan està connectat a una xarxa existent curtcircuit les seves parts individuals —casquilles, barres conductores, travesses, varetes, etc., així com els pneumàtics i barres colectores corresponents— estan sotmeses a una càrrega mecànica sobtada, que té el caràcter d'un impacte.
En els sistemes elèctrics moderns d'alta potència a tensions de 6-20 kV, els corrents de curtcircuit poden assolir valors de fins a 200-300 ka i més, mentre que les forces electrodinàmiques arriben a diverses tones per bus (o autobusos) d'1 a 1,5 m de llarg. ...
En aquestes condicions, la resistència mecànica insuficient d'un o altre element de l'equip elèctric pot provocar un major desenvolupament de l'accident i causar danys greus a l'aparell de commutació. Per tant, per al funcionament fiable de qualsevol instal·lació elèctrica, tots els seus elements han de tenir estabilitat electrodinàmica (resistència mecànica adequada), és a dir, suportar els efectes d'un curtcircuit.
En determinar les forces electrodinàmiques d'acord amb la fórmula anterior, se suposa que el corrent flueix al llarg de l'eix dels cables rodons, el diàmetre dels quals no afecta la magnitud de les forces. Cal tenir en compte que la mida i la forma de la secció transversal dels cables a grans distàncies entre ells no tenen cap efecte notable sobre la magnitud de les forces electrodinàmiques.
Si els cables tenen forma de tires rectangulars i es troben a poca distància entre si, quan la distància a la llum és menor que el perímetre de la cinta, les dimensions de la seva secció transversal poden tenir una influència significativa en les forces electrodinàmiques. Aquesta influència de les dimensions de la secció transversal del conductor es té en compte en els càlculs mitjançant el factor de forma.
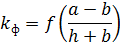
Si cables vius pertanyen al mateix circuit i i1 = i2 = iy llavors la força d'interacció més gran serà igual a
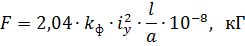
Amb diverses altres formes simples i complexes de cables, és més convenient utilitzar el principi de l'augment de l'energia electromagnètica i les dependències resultants.
Aquestes dependències simples es poden obtenir considerant dos circuits interactius L1 i L2 portats pels corrents i1 i i2. El subministrament d'energia electromagnètica per a aquests circuits serà el següent:
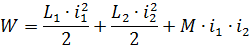
Si, com a resultat de la interacció dels corrents i1 i i2, el bucle del sistema es deforma sota l'acció de forces electrodinàmiques en qualsevol direcció per la quantitat dx, aleshores el treball realitzat per la intensitat de camp Fx serà igual a l'augment. en el subministrament d'energia electromagnètica al sistema per la quantitat dW:
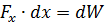
on:
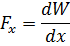
En els casos en què a la pràctica sigui necessari determinar la força electrodinàmica entre parts o costats d'un mateix circuit amb inductància L1-L, la força d'interacció serà:
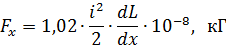
Utilitzant aquesta expressió, determinem les forces electrodinàmiques per a diversos casos senzills però pràcticament importants:
1. Cables paral·lels amb pont.
En els interruptors i seccionadors d'oli, es forma un circuit amb aquesta configuració.
La inductància del bucle serà
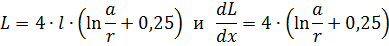
per tant la força que actua sobre la partició és
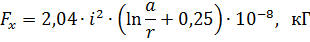
on a és la distància entre els eixos dels cables; r és el radi del cable.
Aquesta expressió dóna les forces electrodinàmiques que actuen sobre el feix de l'interruptor o la fulla de l'interruptor. Faciliten el moviment de la carrera de l'interruptor d'oli quan el corrent està apagat i el repel·leixen quan està encès.
Per tenir una idea de la magnitud de les forces resultants, n'hi ha prou amb dir que, per exemple, en el disjuntor de potència VMB-10 amb un corrent de curtcircuit de 50 kA, la força que actua sobre la travessa és d'uns 200 kg.
2. Un conductor doblegat en angle recte.
Aquesta disposició de conductors s'utilitza normalment en els aparells de commutació per organitzar les barres de les aproximacions i després de l'aparell, també es troba en els seccionadors de bujes.
La inductància del conductor que forma aquest circuit serà:
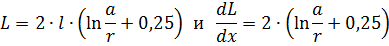
Per tant, l'esforç del lloc es determinarà com en el cas anterior:
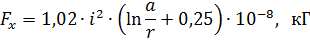
on a és la longitud d'un element mòbil, per exemple, una fulla seccionadora.
Sota l'acció del corrent, el cable doblegat en angle tendeix a redreçar-se, i si un dels seus costats és mòbil, per exemple, la fulla del seccionador, s'han de prendre mesures contra un possible dispar espontani durant un curtcircuit.